对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
(1)如果设正方形OGFN的边长为l,这七块部件的各边长中,从小到大的四个不同值分别为l、x1、x2、x3,那么x1= ;各内角中最小内角是 度,最大内角是 度;用它们拼成的一个五边形如图②,其面积是 ,
(2)请用这副七巧板,既不留下一丝空白,又不相互重叠,拼出2种边数不同的凸多边形,画在下面格点图中,并使凸多边形的顶点落在格点图的小黑点上(格点图中,上下、左右相邻两点距离都为1).
注:不能拼成与图①或②全等的多边形!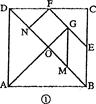


如图,在梯形ABCD中,AB∥CD,∠BAD=90°,以AD为直径的半圆D与BC相切。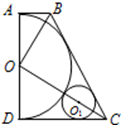
(1)求证:OB⊥OC;
(2)若AD=12,∠BCD=60°,⊙O1与半⊙O外切,并与BC、CD相切,求⊙O1的面积。
关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2。
(1)求k的取值范围;
(2)如果x1+x2-x1x2<-1且k为整数,求k的值。
将两块大小相同的含30°角的直角三角板(∠BAC=∠B′A′C=30°)按图①方式放置,固定三角板A′B′C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A′C交于点E,AC与A′B′交于点F,AB与A′B′相交于点O。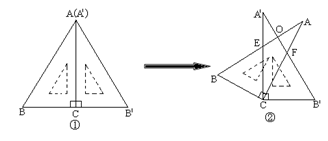
(1)求证:△BCE≌△B′CF;
(2)当旋转角等于30°时,求证:AB⊥A′B′
如图, 为
为 外接圆的直径,
外接圆的直径,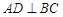 ,垂足为点
,垂足为点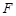 ,
,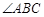 的平分线交
的平分线交 于点
于点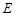 ,连接
,连接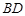 ,
,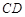 。
。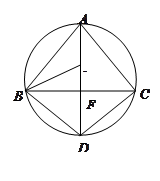
(1) 求证: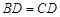 ;
;
(2) 请判断 ,
,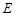 ,
, 三点是否在以
三点是否在以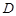 为圆心,以
为圆心,以 为半径的圆上?并说明理由。
为半径的圆上?并说明理由。
先化简再计算: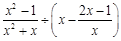 ,其中x是一元二次方程
,其中x是一元二次方程 的正数根。
的正数根。