如图1，抛物线y=－x2＋bx＋c的顶点为Q，与x轴交于A（－1，0）、B(5，0)两点，与y轴交于点C．
(1)求抛物线的解析式及其顶点Q的坐标；
(2)在该抛物线的对称轴上求一点P，使得△PAC的周长最小，请在图中画出点P的位置，并求点P的坐标；
(3)如图2，若点D是第一象限抛物线上的一个动点，过D作DE⊥x轴，垂足为E．
①有一个同学说：“在第一象限抛物线上的所有点中，抛物线的顶点Q与x轴相距最远，所以当点D运动至点Q时，折线D－E－O的长度最长”，这个同学的说法正确吗？请说明理由．
②若DE与直线BC交于点F．试探究：四边形DCEB能否为平行四边形？若能，请直接写出点D的坐标；若不能，请简要说明理由．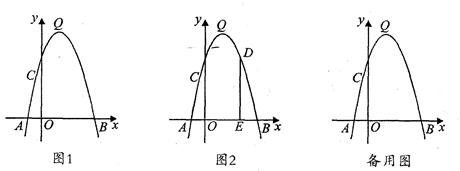
解方程：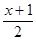
=2+
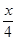
计算：-2+4÷（-2）
如图（1），一正方形纸板ABCD的边长为4，对角线AC、BD交于点O，一块等腰直角三角形的三角板的一个顶点处于点O处，两边分别与线段AB、AD交于点E、F，设BE=
．
（1）若三角板的直角顶点处于点O处，如图（2）．判断三角形EOF的形状
，并说明理由。
（2）在（1）的条件下，若三角形EOF的面积为S，求S关于x的函数关系式。
（3）若三角板的锐角顶点处于点O处，如图（3）．
①若DF=
，求关于的函数关系式，并写出自变量的取值范围；
②探究直线EF与正方形ABCD的内切圆的位置关系，并证明你的结论．
某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该水果的进价为8元/千克，下面是他们在活动结束后的对话.小丽：如果以10元/千克的价格销售，那么每天可售出300千克.
小强：如果以13元/千克的价格销售，那么每天可获取利润750元.
小红：通过调查验证，我发现每天的销售量y（千克）与销售单价x（元）之间存在一次函数关系.
（1）求y（千克）与x（元）（x＞8）的函数关系式；
（2）当销售单价为何值时，该超市销售这种水果每天获取的利润达到800元？【利润＝销售量×（销售单价－进价）】
（3）一段时间后，发现这种水果每天的销售量均不低于225千克．则此时该超市销售这种水果每天利润最大是多少？（x＞8）
如图：AB是⊙O的直径，D、T是圆上两点，且AT平分
，过点T作AD延长线的垂线PQ，垂足为C。
求证：PQ是⊙O的切线。
若⊙O的半径为4，TC=
，求弦AD的长。