如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长;
(3)填空:在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .
(本题8分)
已知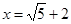 ,
,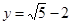 ,求下列各式的值:
,求下列各式的值:
(1)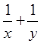 ;
;
(2)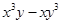 .
.
(每题4分,共16分)
解下列方程:
(1)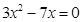
(2)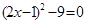
(3)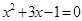
(4)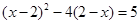
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为 ,两车之间的距离为
,两车之间的距离为 ,图中的折线表示
,图中的折线表示 与
与 之间的函数关系.
之间的函数关系.
根据图象进行以下探究:
(1)请解释图中点B的实际意义;
(2)求慢车和快车的速度;
(3)求线段BC所表示的 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
在矩形纸片ABCD中,AB=6,BC=8, 
(1)将矩形纸片沿BD折叠,使点A落在点E处(如图①),设DE和BC相交于点F,试说明△BDF为等腰三角形,并求BF的长;
(2)将矩形纸片折叠,使B与D重合(如图②)求折痕GH的长。
如图,直线 :y=3x+1与直线
:y=3x+1与直线 :y=mx+n相交于点P(1,b).
:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组 ,请你直接写出它的解;
,请你直接写出它的解;
(3)直线 :y=nx+m是否也经过点P?请说明理由.
:y=nx+m是否也经过点P?请说明理由.