“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了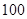 名年龄段在
名年龄段在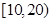 ,
,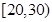 ,
,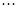 ,
,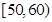 的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
(1)求随机抽取的市民中年龄段在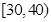 的人数;
的人数;
(2)从不小于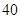 岁的人中按年龄段分层抽样的方法随机抽取
岁的人中按年龄段分层抽样的方法随机抽取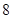 人,求
人,求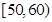 年龄段抽取的人数;
年龄段抽取的人数;
(3)从按(2)中方式得到的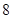 人中再抽取3人作为本次活动的获奖者,记
人中再抽取3人作为本次活动的获奖者,记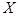 为年龄在
为年龄在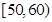 年龄段的人数,求
年龄段的人数,求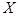 的分布列及数学期望.
的分布列及数学期望.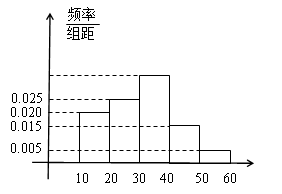
某出版社的11名工人中,有5人只会排版,4人只会印刷,还有2人既会排版又会印刷,现从11人中选4人排版,4人印刷,有多少种不同的选法?
设函数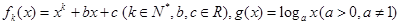 .
.
(1)若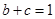 ,且
,且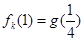 ,求
,求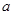 的值;
的值;
(2)若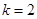 ,记函数
,记函数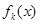 在
在 上的最大值为
上的最大值为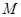 ,最小值为
,最小值为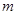 ,求
,求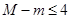 时的
时的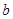 的取值范围;
的取值范围;
(3)判断是否存在大于1的实数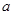 ,使得对任意
,使得对任意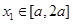 ,都有
,都有 满足等式:
满足等式: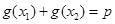 ,且满足该等式的常数
,且满足该等式的常数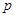 的取值唯一?若存在,求出所有符合条件的
的取值唯一?若存在,求出所有符合条件的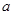 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
定义在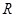 上的函数
上的函数 是最小正周期为2的奇函数, 且当
是最小正周期为2的奇函数, 且当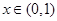 时,
时, 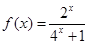 .
.
(1)求 在
在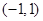 上的解析式;
上的解析式;
(2)用单调性定义证明 在
在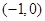 上时减函数;
上时减函数;
(3)当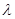 取何值时, 不等式
取何值时, 不等式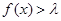 在
在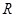 上有解.
上有解.
已知函数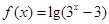 ,
,
(1)求函数 的定义域和值域;
的定义域和值域;
(2)设函数 ,若不等式
,若不等式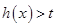 无解,求实数
无解,求实数 的取值范围.
的取值范围.
某企业常年生产一种出口产品,根据预测可知,进入2l世纪以来,该产品的产量平稳增长.记2008年为第1年,且前4年中,第 年与年产量
年与年产量 (万件)之间的关系如下表所示:
(万件)之间的关系如下表所示:
 |
1 |
2 |
3 |
4 |
 |
4.00 |
5.58 |
7.00 |
8.44 |
若 近似符合以下三种函数模型之一:
近似符合以下三种函数模型之一: .
.
(1)找出你认为最适合的函数模型,并说明理由,然后选取08年和10年的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2014年的年产量比预计减少30%,试根据所建立的函数模型,确定2014年的年产量.