已知点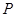 是椭圆
是椭圆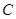 上任一点,点
上任一点,点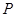 到直线
到直线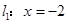 的距离为
的距离为 ,到点
,到点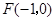 的距离为
的距离为 ,且
,且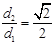 .直线
.直线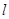 与椭圆
与椭圆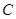 交于不同两点
交于不同两点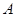 、
、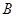 (
(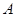 ,
,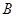 都在
都在 轴上方),且
轴上方),且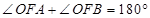 .
.
(1)求椭圆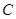 的方程;
的方程;
(2)当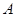 为椭圆与
为椭圆与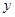 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线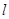 方程;
方程;
(3)对于动直线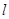 ,是否存在一个定点,无论
,是否存在一个定点,无论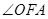 如何变化,直线
如何变化,直线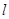 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.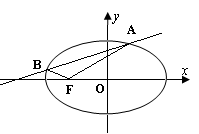
已知函数 ,
, 
(Ⅰ)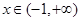 时,证明:
时,证明: ;
;
(Ⅱ)若函数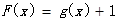 没有零点,求实数
没有零点,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知点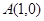 ,点
,点 是圆C:
是圆C: 上的任意一点,,线段
上的任意一点,,线段 的垂直平分线与直线
的垂直平分线与直线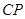 交于点
交于点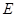 .
.
(1)求点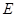 的轨迹方程;
的轨迹方程;
(2)若直线 与点
与点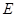 的轨迹有两个不同的交点
的轨迹有两个不同的交点 和
和 ,且原点
,且原点 总在以
总在以 为直径的圆的内部,求实数
为直径的圆的内部,求实数 的取值范围.
的取值范围.
如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况,乙组某个数据的个位数模糊,记为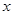 ,已知甲、乙两组的平均成绩相同.
,已知甲、乙两组的平均成绩相同.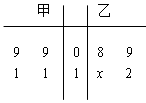
(1)求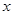 的值,并判断哪组学生成绩更稳定;
的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
如图,在三棱柱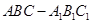 中,
中,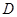 为棱
为棱 的中点,
的中点,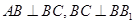 ,
,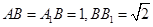 .
.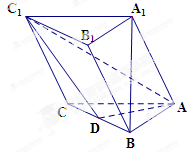
求证:(1)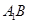
 平面
平面 ;
;
(2)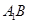 ∥平面
∥平面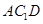 .
.
已知函数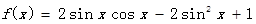 (
( R)
R)
(1)求函数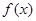 的单调递减区间;
的单调递减区间;
(2)在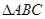 中角
中角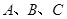 所对的边分别是
所对的边分别是 ,且
,且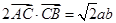 ,
,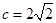 ,
,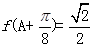 ,
, 为锐角,求
为锐角,求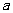 的值.
的值.