若数列 满足条件:存在正整数
满足条件:存在正整数 ,使得
,使得 对一切
对一切 都成立,则称数列
都成立,则称数列 为
为 级等差数列.
级等差数列.
(1)已知数列 为2级等差数列,且前四项分别为
为2级等差数列,且前四项分别为 ,求
,求 的值;
的值;
(2)若 为常数),且
为常数),且 是
是 级等差数列,求
级等差数列,求 所有可能值的集合,并求
所有可能值的集合,并求 取最小正值时数列
取最小正值时数列 的前3
的前3 项和
项和 ;
;
(3)若 既是
既是 级等差数列
级等差数列 ,也是
,也是 级等差数列,证明:
级等差数列,证明: 是等差数列.
是等差数列.
设函数 .
.
(1)求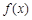 的最小正周期和值域;
的最小正周期和值域;
(2)在锐角△ 中,角
中,角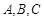 的对边分别为
的对边分别为 ,若
,若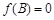 且
且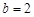 ,
, ,求
,求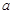 和
和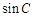 .
.
已知函数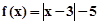 ,
,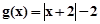 。
。
(1)求不等式 的解集;
的解集;
(2)若不等式 有解,求实数
有解,求实数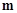 的取值范围。
的取值范围。
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中 轴的正半轴重合,且两坐标系有相同的长度单位,圆C的参数方程为
轴的正半轴重合,且两坐标系有相同的长度单位,圆C的参数方程为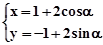 (
( 为参数),点Q的极坐标为
为参数),点Q的极坐标为 。
。
(1)化圆C的参数方程为极坐标方程;
(2)若直线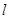 过点Q且与圆C交于M,N两点,求当弦MN的长度为最小时,直线
过点Q且与圆C交于M,N两点,求当弦MN的长度为最小时,直线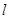 的直角坐标方程。
的直角坐标方程。
如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5。
求:(1)⊙O的半径;(2)s1n∠BAP的值。
已知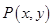 为函数
为函数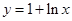 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线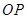 的斜率
的斜率 .
.
(1)若函数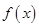 在区间
在区间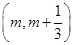
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;
(2)设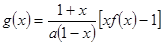 ,若对任意
,若对任意 恒有
恒有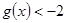 ,求实数
,求实数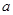 的取值范围.
的取值范围.