如图,椭圆的中心为原点,离心率,一条准线的方程为

(Ⅰ)求该椭圆的标准方程.
(Ⅱ)设动点P满足,其中是椭圆上的点.直线与的斜率之积为-0.5.问:是否存在两个定点,使得为定值.若存在,求的坐标;若不存在,说明理由.
(本小题满分12分)
已知AD是Rt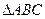 斜边BC的中线,用解析法证明
斜边BC的中线,用解析法证明 .
.
(本小题满分12分)三角形ABC中,AB=6,BC=8,CA=10,绕AB边旋转一周形成一个几何体,(1)求出这个几何体的表面积;(2)求出这个几何体的体积.
(本小题满分10分)通过点A(0,a)的直线 与圆
与圆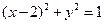 相交于不同的两点B、C,在线段BC上取一点P,使
相交于不同的两点B、C,在线段BC上取一点P,使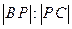 =
=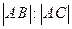 ,设点B在点C的左边,(1)试用a和k表示P点的坐标;(2)求k变化时P点的轨迹;(3)证明不论a取何值时,上述轨迹恒过圆内的一定点.
,设点B在点C的左边,(1)试用a和k表示P点的坐标;(2)求k变化时P点的轨迹;(3)证明不论a取何值时,上述轨迹恒过圆内的一定点.
(本小题满分13分)已知 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边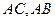 上分别取点
上分别取点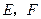 ,使得
,使得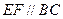 ,把
,把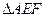 沿直线
沿直线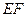 折起,使
折起,使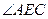 =90°,得四棱锥
=90°,得四棱锥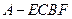 (如图2).在四棱锥
(如图2).在四棱锥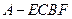 中,
中,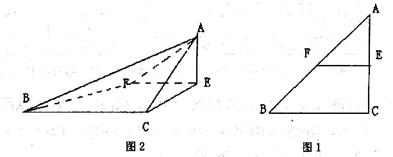
 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  (II)当
(II)当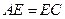 时,试在
时,试在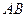 上确定一点G,使得
上确定一点G,使得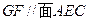 ,并证明你的结论.
,并证明你的结论.




设函数f(x) =" lnx" +ln(2-x)+ ax (a>0).
(1)当a = 1时,求f(x)的单调区间;
(2)若f(x)在(0,1]上的最大值为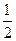 ,求a的值.
,求a的值.