已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm。
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动。当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移。DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5)。解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由。
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由。(图(3)供同学们做题使用)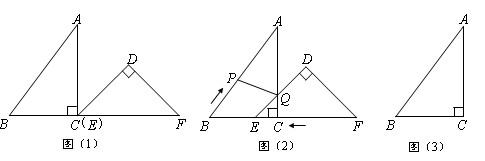
解方程组:
分解因式:
(1) m2+4m+4
(2) a2b-4ab2+3b3
(3)(x2+y2)2-4x2y2
如图(十一)所示,在平面直角坐标系Oxy中,已知点A(-,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C.
(1)求∠ACB的度数;
(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形.若存在,则求出所有 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.
数学课堂上,徐老师出示一道试题:
如图(十)所示,在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
(1)经过思考,小明展示了一种正确的证明过程.请你将证明过程补充完整.
证明:在AB上截取EA=MC,连结EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,∴∠1=∠2.
又CN平分∠ACP,∠4=∠ACP=60°.∴∠MCN=∠3+∠4=120°…………①
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM.
∴△BEM为等边三角形.∴∠6=60°.
∴∠5=180°-∠6=120°.………②
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵
∴△AEM≌△MCN (ASA).∴AM=MN.
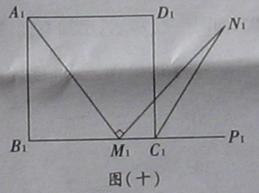
(2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1.是否还成立?(直接写出答案,不需要证明)
(3) 若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠AnMnNn=°时,结论AnMn=MnNn仍然成立?(直接写出答案,不需要证明)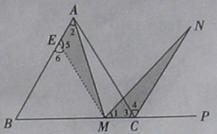
为庆祝建党90周年,某学校欲按如下规则组建一个学生合唱团参加我市的唱红歌比赛.
规则一:合唱队的总人数不得少于50人,且不得超过55人.
规则二:合唱队的队员中,九年级学生占合唱团宗人数的,八年级学生占合唱团总人数的,余下的为七年级学生.请求出该合唱团中七年级学生的人数.