已知椭圆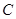 :
: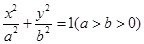 经过点
经过点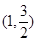 ,其离心率
,其离心率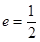 .
.
(1)求椭圆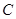 的方程;
的方程;
(2)过坐标原点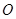 作不与坐标轴重合的直线
作不与坐标轴重合的直线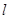 交椭圆
交椭圆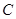 于
于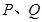 两点,过
两点,过 作
作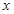 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接 并延长交椭圆
并延长交椭圆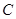 于点
于点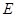 ,试判断随着
,试判断随着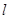 的转动,直线
的转动,直线 与
与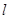 的斜率的乘积是否为定值?说明理由.
的斜率的乘积是否为定值?说明理由.
已知一对夫妇有且只有两个孩子,其中一个是女孩,请问,另一个孩子也是女孩的概率是多少?
已知有一对夫妇,已经有一个女孩了,现在妈妈又怀孕了,请问这次怀孕生女孩的概率是多少?
掷三颗骰子,
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率.
将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之积是6的倍数的概率;
(2)以第一次向上的点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在直线x-y=3的下方区域的概率.
每次抛掷一枚骰子
(1)连掷2次,求向上的数不同的概率;
(2)连掷2次,求向上的数之和为6的概率;
(3)连掷5次,求向上的数为奇数恰好出现3次的概率。