每次抛掷一枚骰子
(1)连掷2次,求向上的数不同的概率;
(2)连掷2次,求向上的数之和为6的概率;
(3)连掷5次,求向上的数为奇数恰好出现3次的概率。
请从下面具体的例子中说明几个基本的程序框和它们各自表示的功能,并把它填在相应的括号内.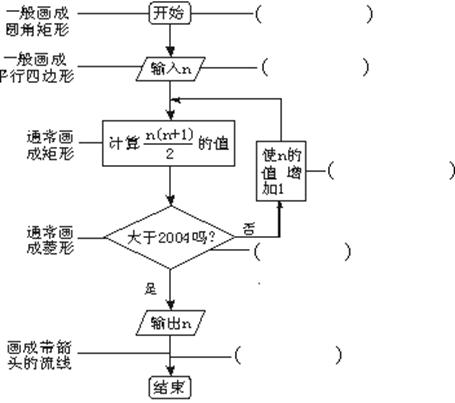
写出用二分法求方程x3-x-1=0在区间[1,1.5]上的一个解的算法(误差不
超过0.001),并画出相应的程序框图及程序.
某城市现有人口总数为100万人,如果年自然增长率为1.2%,试解答下列问题:
(1)写出该城市人口数y(万人)与年份x(年)的函数关系式;
(2)表示计算10年以后该城市人口总数的算法;
(3)用流程图表示计算大约多少年以后该城市人口将达到120万人的算法。
试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。
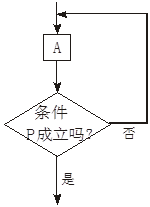
下面循环结构的程序框图中,哪一个是当型循环的程序框图?哪一个是直到型循
环的程序框图?
(1)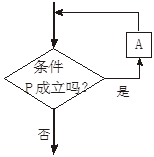
(2)