已知函数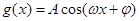 +
+ 的部分图象如图所示.
的部分图象如图所示.
(1)将函数 的图象保持纵坐标不变,横坐标向右平移
的图象保持纵坐标不变,横坐标向右平移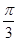 个单位后得到函数
个单位后得到函数 的图像,求函数
的图像,求函数 在
在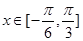 上的值域;
上的值域;
(2)求使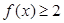 的
的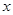 的取值范围的集合.
的取值范围的集合.
已知函数f(x)= ,x∈[1,+∞
,x∈[1,+∞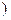
(1)当a=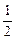 时,求函数f(x)的最小值。
时,求函数f(x)的最小值。
(2)若对任意x∈[1,+∞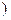 ,f(x)>0恒成立,试求实数a的取值范围。
,f(x)>0恒成立,试求实数a的取值范围。
已知倾斜角为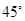 的直线
的直线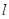 过点
过点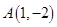 和点
和点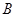 ,点
,点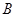 在第一象限,
在第一象限,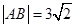 。
。
(1)求点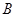 的坐标;
的坐标;
(2)若直线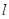 与双曲线
与双曲线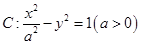 相交于
相交于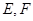 两点,且线段
两点,且线段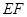 的中点坐标为
的中点坐标为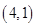 ,求
,求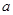 的值;
的值;
(3)对于平面上任一点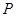 ,当点
,当点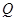 在线段
在线段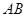 上运动时,称
上运动时,称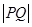 的最小值为
的最小值为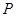 与线段
与线段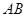 的距离。已知
的距离。已知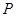 在
在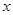 轴上运动,写出点
轴上运动,写出点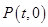 到线段
到线段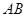 的距离
的距离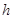 关于
关于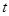 的函数关系式。
的函数关系式。
已知函数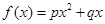 ,其中p>0,p+q>1。对于数列
,其中p>0,p+q>1。对于数列 ,设它的前n项之和为
,设它的前n项之和为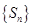 ,且
,且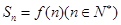 。
。
(1)求数列 的通项公式;
的通项公式;
(2)证明: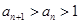 (3)证明:点
(3)证明:点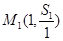 ,
,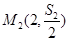 ,
,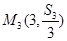 ,
, ,
,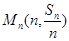 共线
共线
在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x)。某公司每月最多生产100台报警系统装置,生产x台的收入函数为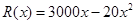 (单位:元),其成本函数为
(单位:元),其成本函数为 (单位:元),利润是收入与成本之差。
(单位:元),利润是收入与成本之差。
(1)求利润函数P(x)及边际利润函数MP(x);
(2)利润函数P(x)与边际利润函数MP(x)是否具有相等的最大值?
(3)你认为本题中边际利润函数MP(x)取最大值的实际意义是什么?
如图,四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形,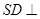 底面
底面 ,
, 。
。
(1)求证: ;
;
(2)设棱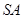 的中点为
的中点为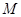 ,求异面直线
,求异面直线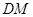 与
与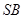 所成角的大小;
所成角的大小;