已知数列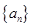 满足
满足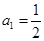 ,
,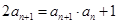 .
.
(1)求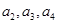 的值,由此猜测
的值,由此猜测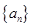 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(2)证明: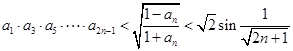 .
.
如图,某兴趣小组测得菱形养殖区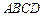 的固定投食点
的固定投食点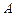 到两条平行河岸线
到两条平行河岸线 的距离分别为4m、8m,河岸线
的距离分别为4m、8m,河岸线 与该养殖区的最近点
与该养殖区的最近点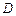 的距离为1m,
的距离为1m, 与该养殖区的最近点
与该养殖区的最近点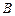 的距离为2m.
的距离为2m.
(1)如图甲,养殖区在投食点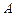 的右侧,若该小组测得
的右侧,若该小组测得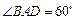 ,请据此算出养殖区的面积;
,请据此算出养殖区的面积;
(2)如图乙,养殖区在投食点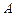 的两侧,试在该小组未测得
的两侧,试在该小组未测得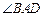 的大小的情况下,估算出养殖区的最小面积.
的大小的情况下,估算出养殖区的最小面积.
在△ABC中,角A,B,C的对边分别是a,b,c,且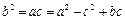 .
.
(1)求 的值;
的值;
(2)试判断△ABC的形状,并说明理由
设定义在 上的函数
上的函数
 的最小正周期为
的最小正周期为 .
.
(1)若 ,
, ,求
,求 的最大值;
的最大值;
(2)若 ,
, ,求
,求 的值
的值
平面直角坐标系 中,已知向量
中,已知向量 且
且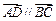 .
.
(1)求 与
与 之间的关系式;
之间的关系式;
(2)若 ,求四边形
,求四边形 的面积
的面积
已知函数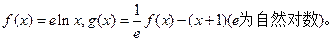
(1)求函数 的极大值;(2)
的极大值;(2)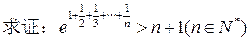
(3)对于函数 定义域上的任意实数
定义域上的任意实数 ,若存在常数
,若存在常数 ,使得
,使得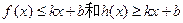 都成立,则称直线
都成立,则称直线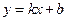 为函数
为函数 的分界线。设
的分界线。设 ,试探究函数
,试探究函数 是否存在“分界线”?若存在,请给予证明,并求出
是否存在“分界线”?若存在,请给予证明,并求出 的值;若不存在,请说明理由
的值;若不存在,请说明理由