在雅礼中学组织的“雅礼杯”篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是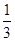 ,
,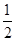 .两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
.两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
(1)求3次投篮的人依次是甲、甲、乙的概率;
(2)若投篮命中一次得1分,否则得0分. 用ξ表示甲的总得分,求ξ的分布列和数学期望.
袋中有大小相 同的4个红球与2个白球。
同的4个红球与2个白球。
(1)若从袋中依次不放回取出一个球,求第三次取出白球的概率;
( 2)若从袋中依次不放回取出
2)若从袋中依次不放回取出 一个球,求第一次取出红球的条件下第三次仍取出红球的概率。
一个球,求第一次取出红球的条件下第三次仍取出红球的概率。
(3)若从中有放回的依次取出一个球,记6次取球中取出红球的次数为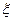 ,求
,求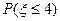 与
与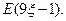
设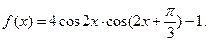
(1)求 的最小值及此时x的取值集合;
的最小值及此时x的取值集合;
(2)把 的图象向右平移
的图象向右平移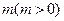 个单位后所得图象关于y轴对称,求m的最小值。
个单位后所得图象关于y轴对称,求m的最小值。
.(本题满分9分)
已知:函数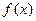 对一切实数
对一切实数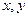 都有
都有
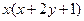 成立,且
成立,且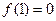 .(1)求
.(1)求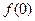 的值(2)求
的值(2)求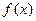 的解析式
的解析式
(3)已知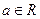 ,设P:当
,设P:当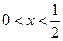 时,不等式
时,不等式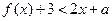 恒成立;Q:当
恒成立;Q:当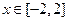 时,
时,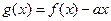 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的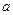 的集合记为
的集合记为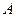 ,满足Q成立的
,满足Q成立的
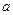 的集合记为
的集合记为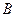 ,求
,求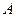 ∩
∩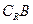 (
( 为全集)
为全集)
(本题8分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表 示为投资的函数,并写出它们的函数关系式
示为投资的函数,并写出它们的函数关系式
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能是企业获得最大利润,其最大利润约为多少万元(精确到1万元).

(本题9分)已知函数 .
.
(1) 判断函数的奇偶性; (2) 求该函数的值域;⑶ 利用定义法证明 是
是 上的增函数
上的增函数