如图甲所示,空间存在一范围足够大的垂直于xOy平面向外的匀强磁场,磁感应强度大小为B,让质量为m、电量为q(q>0)的粒子从坐标原点O沿xOy平面以不同的初速度大小和方向入射到该磁场中。不计粒子重力和粒子间的影响。
(1)若粒子以初速度v1沿y轴正向入射,恰好能经过x轴上的A(a,0)点,求v1的大小;
(2)已知某一粒子的初速度大小为v(v>v1),为使该粒子仍能经过A(a,0)点,其入射角θ(粒子初速度与x轴正向的夹角)有几个,并求出对应的sinθ值;
(3)如图乙所示,若在此空间再加入沿y轴正向、大小为E的匀强电场,一粒子从O点以初速v0沿y轴正向发射。研究表明:该粒子将在xOy平面内做周期性运动,且在任一时刻,粒子速度的x分量vx与其所在位置的y坐标成正比,比例系数与场强大小E无关。求该粒子运动过程中的最大速度值vm?
重力势能EP=mgh实际上是万有引力势能在地面附近的近似表达式,其更精确的表达式应为 。式中的G为万有引力恒量,M为地球质量,m为物体的质量,r为物体到地心的距离,并以无限远处的引力势能为零势能。一颗质量为m的地球卫星,在离地高度为H处环绕地球做匀速圆周运动。已知地球的半径为R,地球表面的重力加速度为g,地球质量未知。试求:
。式中的G为万有引力恒量,M为地球质量,m为物体的质量,r为物体到地心的距离,并以无限远处的引力势能为零势能。一颗质量为m的地球卫星,在离地高度为H处环绕地球做匀速圆周运动。已知地球的半径为R,地球表面的重力加速度为g,地球质量未知。试求:卫星做匀速圆周运动的线速度;
卫星的引力势能;
卫星的机械能;
若要使卫星能飞离地球(飞到引力势能为零的地方),则卫星至少要具有多大的初速度从地面发射?
如图所示,长度为l的轻绳上端固定在O点,下端系一质量为m的小球(小球的大小可以忽略).在水平拉力F的作用下,轻绳与竖直方向的夹角为α,小球保持静止,画出此时小球的受力图,并求力F的大小.
由图示位置撤去力F静止释放小球,求当小球通过最低点时的速度大小及轻绳对小球的拉力.不计空气阻力.

在某城市的一条道路上,规定车辆行驶速度不得超过40km/h。在一次交通事故中,肇事车是一辆卡车,量得这辆卡车紧急刹车(车轮被抱死)时留下的刹车痕迹长为9m,已知该卡车紧急刹车时的加速度大小是8m/s2。判断该车是否超速。
求刹车时间。
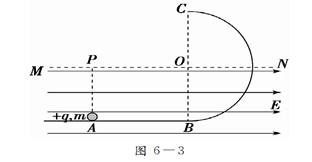
如图所示,光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接.在过圆心O的水平界面MN的下方分布有水平向右的匀强电场.现有一质量为m、电荷量为+q的小球从水平轨道上A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方,如图.小球可视为质点,小球运动到C点之前电荷量保持不变,经过C点后电荷量立即变为零).已知AB间距离为2R,重力加速度为g.在上述运动过程中,求:电场强度E的大小;
小球在圆轨道上运动时的最大速率;
小球对圆轨道的最大压力的大小.
一个灯泡L,标有“6V 12W”字样,一台直流电动机D,其线圈电阻为 ,把L与D并联,当电动机正常工作时,灯泡也正常发光;把L与D串联,当电动机正常工作时,灯泡的实际功率是额定功率的3/4。求这台电动机正常工作时转化为机械能的功率。(假定灯泡电阻保持不变)
,把L与D并联,当电动机正常工作时,灯泡也正常发光;把L与D串联,当电动机正常工作时,灯泡的实际功率是额定功率的3/4。求这台电动机正常工作时转化为机械能的功率。(假定灯泡电阻保持不变)