已知函数f(x)=3x-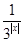 .
.
(1)若f(x)=2,求x的值;
(2)判断x>0时,f(x)的单调性;
(3)若3tf(2t)+mf(t)≥0对于t∈ 恒成立,求m的取值范围.
恒成立,求m的取值范围.
如图,直角梯形ABMN中,∠NAB=90°,AN∥BM,AB=2,AN= ,BM=
,BM= ,椭圆C以A,B为焦点且过点N.
,椭圆C以A,B为焦点且过点N.
(1)建立适当的坐标系,求椭圆C方程;
(2)若点E满足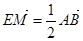 ,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
如图,ABCD是边长为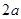 的正方形,ABEF是矩形,且二面角C
的正方形,ABEF是矩形,且二面角C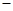 AB
AB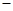 F是直二面角,
F是直二面角,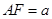 ,G是EF的中点,
,G是EF的中点,
(1)求GB与平面AGC所成角的正弦值.
(2)求二面角B—AC—G的余弦值.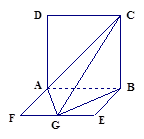
已知 ,讨论方程
,讨论方程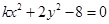 所表示的圆锥曲线类型,并求其焦点坐标
所表示的圆锥曲线类型,并求其焦点坐标
某班同学利用国庆节进行社会实践,对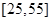 岁的人群随机抽取
岁的人群随机抽取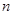 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图: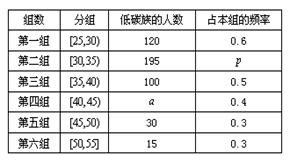
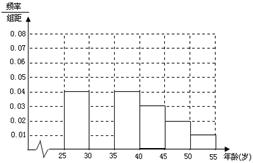
(Ⅰ)补全频率分布直方图并求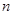 、
、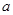 、
、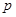 的值;
的值;
(Ⅱ)试由各年龄段人数频率分布直方图估计这随机抽取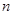 人的平均年龄。
人的平均年龄。
设p:实数x满足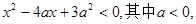 q:实数x满足
q:实数x满足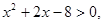 且
且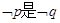 的必要不充分条件,求a的取值范围。
的必要不充分条件,求a的取值范围。