已知a=(1,2),b=(-2,n) (n>1),a与b的夹角是45°.
(1)求b;
(2)若c与b同向,且a与c-a垂直,求c.
已知数列{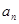 }是公差不为零的等差数列,
}是公差不为零的等差数列,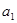 =" 1" ,且
=" 1" ,且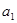 ,
,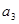 ,
,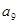 成等比数列.
成等比数列.
(1)求数列{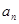 }的通项公式 ;
}的通项公式 ;
(2)求数列{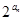 }的前n项和
}的前n项和 .
.
(1)设a > 0 , b > 0 ,求证:  a + b ;
a + b ;
(2)设x,y都是正实数 ,且x + y =" 1" ,求证:(1+  )(1+
)(1+ 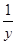 ) ≥ 9 .
) ≥ 9 .
如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2, ,垂足为E,且E是OB的中点,求BC的长。
,垂足为E,且E是OB的中点,求BC的长。
在正方体 中,D是AC的中点,E是线段D
中,D是AC的中点,E是线段D O上一点,且
O上一点,且
(1)若 ,求异面直线DE与CD
,求异面直线DE与CD 所成角的余弦值;
所成角的余弦值;
(2)若面CDE 面CD
面CD O,求
O,求 的值
的值
|
在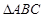 中,角A,B,C所对的边分别为a,b,c,a=1,c=
中,角A,B,C所对的边分别为a,b,c,a=1,c=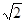 ,
,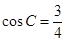
(1)求
(2)求 的值
的值
(3)求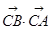 的值
的值