(Ⅰ)设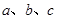 为正数,且
为正数,且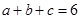 ,求证:
,求证: ;
;
(Ⅱ)设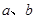 为正数,
为正数, ,求证:
,求证: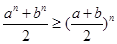
如图,一人在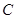 地看到建筑物
地看到建筑物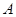 在正北方向,另一建筑物
在正北方向,另一建筑物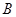 在北偏西
在北偏西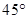 方向,此人向北偏西
方向,此人向北偏西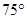 方向前进
方向前进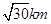 到达
到达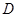 处,看到
处,看到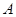 在他的北偏东
在他的北偏东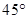 方向,
方向,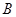 在北偏东
在北偏东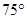 方向,试求这两座建筑物之间的距离.
方向,试求这两座建筑物之间的距离.
.(14分)已知椭圆 +
+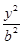 =1(a>b>0)的左、右焦点分别是F1(-c,0),F2(c,0),Q是椭圆外的动点,满足
=1(a>b>0)的左、右焦点分别是F1(-c,0),F2(c,0),Q是椭圆外的动点,满足 =2a.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
=2a.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足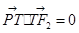 ,
,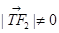
(1)设x为点P的横坐标,证明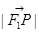 =a+
=a+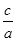 x;
x;
(2)求点T的轨迹C的方程;
(3)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=b2?若存在,求∠F1MF2的正切值;若不存在,请说明理由.
设二次函数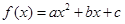 (a>0),方程
(a>0),方程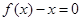 的两个根
的两个根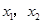
满足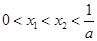 . (1)
. (1) ,求
,求 的值。
的值。
(2)设函数 的图象关于直线
的图象关于直线 对称,证明:
对称,证明:
(3)当x∈(0,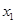 )时,证明x<
)时,证明x< <
<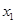 ;
;
、已知命题p:方程a2x2+ax-2=0在[-1,1]上有解:命题q:只有一个
实数 x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求a的取值范围.
x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求a的取值范围.