第十二届全国人民代表大会第二次会议和政协第十二届全国委员会第二次会议,2014年3月在北京召开.为了做好两会期间的接待服务工作,中国人民大学学生实践活动中心从7名学生会干部(其中男生4人,女生3人)中选3人参加两会的志愿者服务活动.
(1)所选3人中女生人数为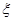 ,求
,求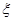 的分布列及数学期望:
的分布列及数学期望:
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.
【2015高考新课标2,理23】选修4-4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 (
( 为参数,
为参数, ),其中
),其中 ,在以
,在以 为极点,
为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 ,曲线
,曲线 .
.
(Ⅰ)求 与
与 交点的直角坐标;
交点的直角坐标;
(Ⅱ)若 与
与 相交于点
相交于点 ,
, 与
与 相交于点
相交于点 ,求
,求 的最大值.
的最大值.
【2015高考新课标2,理22】选修4—1:几何证明选讲
如图, 为等腰三角形
为等腰三角形 内一点,圆
内一点,圆 与
与 的底边
的底边 交于
交于 、
、 两点与底边上的高
两点与底边上的高 交于点
交于点 ,与
,与 、
、 分别相切于
分别相切于 、
、 两点.
两点.
(Ⅰ)证明: ;
;
(Ⅱ)若 等于
等于 的半径,且
的半径,且 ,求四边形
,求四边形 的面积.
的面积.
【2015高考上海,理19】如图,在长方体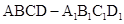 中,
中,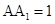 ,
,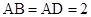 ,
,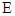 、
、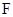 分别是
分别是 、
、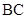 的中点.证明
的中点.证明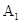 、
、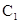 、
、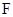 、
、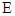 四点共面,并求直线
四点共面,并求直线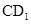 与平面
与平面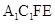 所成的角的大小.
所成的角的大小.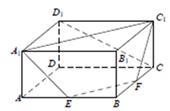
【2015高考湖南,理19】如图,已知四棱台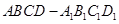 上、下底面分别是边长为3和6的正方形,
上、下底面分别是边长为3和6的正方形,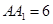 ,且
,且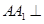 底面
底面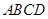 ,点
,点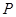 ,
,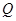 分别在棱
分别在棱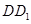 ,BC上.
,BC上.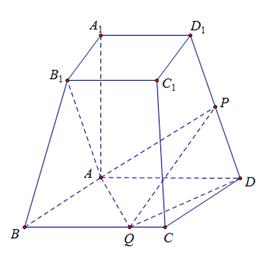
(1)若P是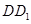 的中点,证明:
的中点,证明: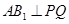 ;
;
(2)若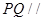 平面
平面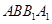 ,二面角
,二面角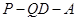 的余弦值为
的余弦值为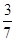 ,求四面体
,求四面体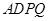 的体积.
的体积.
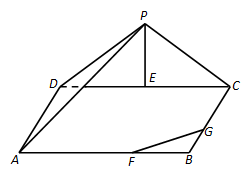
【2015高考广东,理18】如图,三角形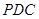 所在的平面与长方形
所在的平面与长方形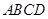 所在的平面垂直,
所在的平面垂直,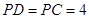 ,
,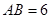 ,
,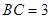 .点
.点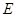 是
是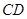 边的中点,点
边的中点,点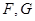 分别在线段
分别在线段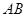 、
、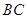 上,且
上,且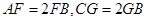 .
.
(1)证明: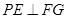 ;
;
(2)求二面角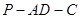 的正切值;
的正切值;
(3)求直线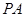 与直线
与直线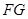 所成角的余弦值.
所成角的余弦值.