为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 |
相关人数 |
抽取人数 |
| A |
16 |
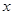 |
| B |
12 |
3 |
| C |
8 |
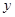 |
(Ⅰ)确定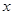 与
与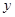 的值;
的值;
(Ⅱ)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
在△ABC中,角A、B、C所对的边分别为a、b、c(其中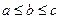 ),设向量
),设向量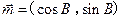 ,
,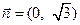 ,且向量
,且向量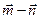 为单位向量.
为单位向量. (1)求∠B的大小;
(1)求∠B的大小;
(2)若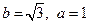 ,求△ABC的面积.
,求△ABC的面积.
已知数列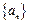 满足:
满足: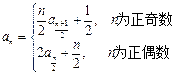 .
.
(Ⅰ)问数列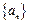 是否为等差数列或等比数列?说明理由;
是否为等差数列或等比数列?说明理由;
(Ⅱ)求证:数列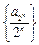 是等差数列,并求数列
是等差数列,并求数列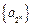 的通项公式;
的通项公式;
(Ⅲ)设 ,求数列
,求数列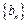 的前
的前 项和
项和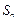 .
.
已知圆 和椭圆
和椭圆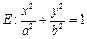
 的一个公共点为
的一个公共点为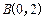 .
.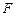 为椭圆
为椭圆 的右焦点,直线
的右焦点,直线 与圆
与圆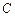 相切于点
相切于点 .
.
(Ⅰ)求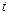 值和椭圆
值和椭圆 的方程;
的方程;
(Ⅱ)圆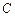 上是否存在点
上是否存在点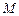 ,使
,使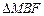 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点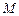 的坐标.
的坐标.
已知函数 ,其中
,其中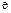 是自然对数的底数.
是自然对数的底数.
(Ⅰ)求函数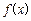 的图象在
的图象在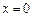 处的切线方程;
处的切线方程;
(Ⅱ)求函数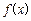 在区间
在区间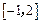 上的最大值与最小值.
上的最大值与最小值.
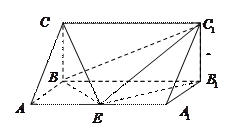
一个三棱柱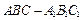 直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设
直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设 、
、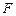 分别为
分别为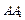 和
和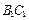 的中点.
的中点.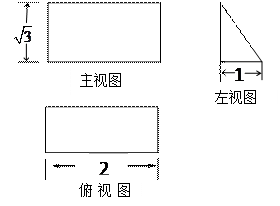
(Ⅰ)求几何体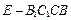 的体积;
的体积;
(Ⅱ)证明: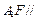 平面
平面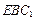 ;
;
(Ⅲ)证明:平面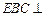 平面
平面 .
.