(本小题满分12分)一工厂生产甲、乙、丙三种样式的杯子,每种样式均有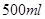 和
和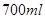 两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取
两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取 个,其中有甲样式杯子
个,其中有甲样式杯子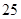 个.
个.
| 型号 |
甲样式 |
乙样式 |
丙样式 |
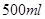 |
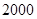 |
 |
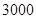 |
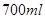 |
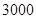 |
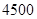 |
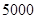 |
(1)求 的值;
的值;
(2)用分层抽样的方法在甲样式杯子中抽取一个容量为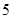 的样本,从这个样本中任取
的样本,从这个样本中任取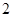 个杯子,求至少有
个杯子,求至少有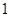 个
个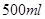 杯子的概率.
杯子的概率.
(本小题满分8分)
⑴已知△ABC三个顶点的坐标分别为A(4,1),B(0,3),C(2,4),边AC的中点为D,求AC边上中线BD所在的直线方程并化为一般式;
⑵已知圆C的圆心是直线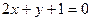 和
和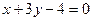 的交点上且与直线
的交点上且与直线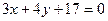 相切,求圆C的方程.
相切,求圆C的方程.
已知中心在原点的椭圆的一个焦点为(0 , ),且过点
),且过点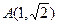 ,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。
,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。
(1)求椭圆的标准方程;
(2)求证:直线BC的斜率为定值,并求这个定值。
(3)求三角形ABC的面积最大值。
如图,抛物线顶点在原点,圆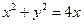 的圆心是抛物线的焦点,直线
的圆心是抛物线的焦点,直线 过抛物线的焦点,且斜率为2,直线
过抛物线的焦点,且斜率为2,直线 交抛物线与圆依次为
交抛物线与圆依次为 、
、 、
、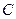 、
、 四点.
四点.
(1)求抛物线的方程.
(2)求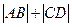 的值.
的值.
已知命题:“ ,都有不等式
,都有不等式 成立”是真命题。
成立”是真命题。
(1)求实数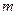 的取值集合
的取值集合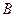 ;
;
(2)设不等式 的解集为
的解集为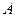 ,若
,若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数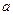 的取值范围.
的取值范围.
已知
(I)当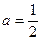 时,解不等式
时,解不等式 ;
;
(II)若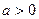 ,解关于x的不等式
,解关于x的不等式 。
。