如图,抛物线顶点在原点,圆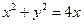 的圆心是抛物线的焦点,直线
的圆心是抛物线的焦点,直线 过抛物线的焦点,且斜率为2,直线
过抛物线的焦点,且斜率为2,直线 交抛物线与圆依次为
交抛物线与圆依次为 、
、 、
、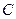 、
、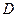 四点.
四点.
(1)求抛物线的方程.
(2)求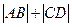 的值.
的值.
建造一个容积为50 ,高为2
,高为2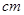 长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?
长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?
解关于的不等式: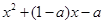 <
< .
.
如图是一个从 的”闯关”游戏.
的”闯关”游戏. 
规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于 则闯关成功.
则闯关成功.
(1)求闯第一关成功的概率;
(2)记闯关成功的关数为随机变量X,求X的分布列和期望。
如图所示,在三棱锥PABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.
(1)求证:AB⊥平面PBC;
(2)设AB=BC,直线PA与平面ABC所成的角为45°,求异面直线AP与BC所成的角;
(3)在(2)的条件下,求二面角C-PA-B的余弦值.
已知 的展开式前三项中的
的展开式前三项中的 的系数成等差数列.
的系数成等差数列.
(1)展开式中所有的 的有理项为第几项?
的有理项为第几项?
(2)求展开式中系数最大的项.