已知双曲线 与椭圆
与椭圆 有相同的焦点,点
有相同的焦点,点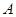 、
、 分别是椭圆的右、右顶点,若椭圆经过点
分别是椭圆的右、右顶点,若椭圆经过点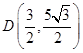 .
.
(1)求椭圆的方程;
(2)已知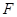 是椭圆的右焦点,以
是椭圆的右焦点,以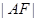 为直径的圆记为
为直径的圆记为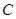 ,过点
,过点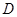 引圆
引圆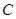 的切线,求此切线的方程;
的切线,求此切线的方程;
(3)设 为直线
为直线 上的点,
上的点, 是圆
是圆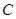 上的任意一点,是否存在定点
上的任意一点,是否存在定点 ,使得
,使得 ?若存在,求出定点
?若存在,求出定点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
已知复数z=x+yi(x,y∈R)在复平面上对应的点为M.
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中随机取一个数作为y,求复数z为纯虚数的概率.
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组: 所表示的平面区域内的概率.
所表示的平面区域内的概率.
设函数f(x)=x2+bx+c,其中b,c是某范围内的随机数,分别在下列条件下,求事件A“f(1)≤5且f(0)≤3”发生的概率.
(1)若随机数b,c∈{1,2,3,4}.
(2)已知随机函数Rand( )产生的随机数的范围为{x|0≤x≤1},b,c是算法语句b="4*Rand(" )和c="4*Rand(" )的执行结果.(注:符号“*”表示“乘号”)
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1,A2,A3,A4是道路网中位于一条对角线上的4个交汇处,今在道路网M,N处的甲、乙两人分别要到N,M处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止.
(1)求甲经过A2的概率.
(2)求甲、乙两人相遇经A2点的概率.
(3)求甲、乙两人相遇的概率.
为了提高食品的安全度,某食品安检部门调查了一个海水养殖场的养殖鱼的有关情况,安检人员从这个海水养殖场中不同位置共捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据进行统计得下表.若规定超过正常生长速度(1.0~1.2 kg/年)的比例超过15%,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题.
| 鱼的 质量 |
[1.00, 1.05) |
[1.05, 1.10) |
[1.10, 1.15) |
[1.15, 1.20) |
[1.20, 1.25) |
[1.25, 1.30) |
| 鱼的 条数 |
3 |
20 |
35 |
31 |
9 |
2 |
(1)根据数据统计表,估计数据落在[1.20,1.30)中的概率约为多少,并判断此养殖场所饲养的鱼是否存在问题?
(2)上面捕捞的100条鱼中间,从质量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条的概率.
某校高三某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下图,据此解答如下问题: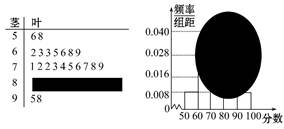
(1)求分数在[50,60)的频率及全班的人数.
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高.
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份在[90,100]之间的概率.