已知向量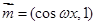 ,
,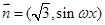 (
(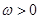 ),函数
),函数 ,且
,且 图象上一个最高点为
图象上一个最高点为
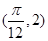 ,与
,与 最近的一个最低点的坐标为
最近的一个最低点的坐标为 .
.
(1)求函数 的解析式;
的解析式;
(2)设 为常数,判断方程
为常数,判断方程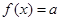 在区间
在区间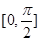 上的解的个数;
上的解的个数;
(3)在锐角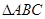 中,若
中,若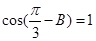 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)如图,在长方体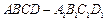
中,已知底面ABCD是边长为1的正方形,侧棱 ,P是侧棱
,P是侧棱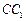 上的一点,
上的一点,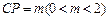 .
.
(Ⅰ)试问直线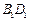 与AP能否垂直?并说明理由;
与AP能否垂直?并说明理由;
(Ⅱ)试确定m,使直线AP与平面BDD1B1所成角为60º;(Ⅲ)若m=1,求平面PA1D1与平面PAB所成角的大小.
(本小题满分12分)如图,在铁路建设中需要确
定隧道的长度和隧道两端的施工方向.已测得隧道两
端的两点A、B到某一点C的距离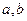 及
及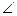 ACB=
ACB=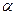 ,求A、B两点间的距离,以及
,求A、B两点间的距离,以及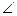 ABC、
ABC、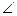 BAC.
BAC.
(本小题满分14分)下图是一个三角形数阵.从第二行起每一个数都等于它肩上两个数的和,第 行的第一个数为
行的第一个数为 .
.
(Ⅰ)写出 与
与 的递推关系,并求
的递推关系,并求 ;
;
(Ⅱ)求第 行所有数的和
行所有数的和 ;
;
(Ⅲ)求数阵中所有数的和 ;并证明:当
;并证明:当 时,
时, .
.
(本小题满分13分)已知两定点 ,平面上动点
,平面上动点 满足
满足 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 的直线
的直线 与
与 交于
交于 两点,且
两点,且 ,当
,当 时,求直线
时,求直线 的斜率
的斜率 的取值范围.
的取值范围.
(本小题满分12分)如图,用一块形状为半椭圆
 的铁皮截取一个以短轴
的铁皮截取一个以短轴 为底的等腰梯形
为底的等腰梯形 ,问:怎样截才能使所得等腰梯形
,问:怎样截才能使所得等腰梯形 的面积最大?
的面积最大?