如图,直三棱柱ABC-A1B1C1中, D、E分别是AB,BB1的中点.
(1)证明: BC1//平面A1CD;
(2)设AA1="AC=CB=1," AB= ,求三棱锥D一A1CE的体积.
,求三棱锥D一A1CE的体积.
如图,在矩形 中,点
中,点 为边
为边 上的点,点
上的点,点 为边
为边 的中点,
的中点, ,现将
,现将 沿
沿 边折至
边折至 位置,且平面
位置,且平面 平面
平面 .
.
(1) 求证:平面 平面
平面 ;
;
(2) 求二面角 的大小.
的大小.
已知二次函数
 (
( ),若
),若 是从区间
是从区间 中随机抽取的一个数,
中随机抽取的一个数, 是从区间
是从区间 中随机抽取的一个数,求方程
中随机抽取的一个数,求方程 没有实数根的概率.
没有实数根的概率.
如图,在四棱锥 中,
中, 为正三角形,
为正三角形, 平面
平面 ,
, 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 .
.
已知三点 ,
, ,
, .
.
(1)求 与
与 的夹角;
的夹角;
(2)求 在
在 方向上的投影.
方向上的投影.
定义在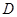 上的函数
上的函数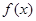 ,如果满足:对任意
,如果满足:对任意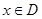 ,存在常数
,存在常数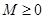 ,都有
,都有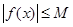 成立,则称
成立,则称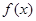 是
是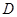 上的有界函数,其中
上的有界函数,其中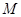 称为函数
称为函数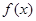 的一个上界.
的一个上界.
已知函数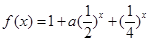 ,
,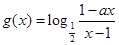 .
.
(1)若函数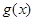 为奇函数,求实数
为奇函数,求实数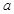 的值;
的值;
(2)在(1)的条件下,求函数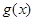 在区间
在区间 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数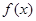 在
在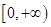 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数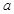 的取值范围.
的取值范围.