在平面直角坐标系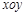 中,已知椭圆的焦点在
中,已知椭圆的焦点在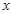 轴上,离心率为
轴上,离心率为 ,且经过点
,且经过点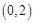 .
.
(1)求椭圆的标准方程;
(2) 以椭圆的长轴为直径作圆 ,设
,设 为圆
为圆 上不在坐标轴上的任意一点,
上不在坐标轴上的任意一点, 为
为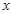 轴上一点,过圆心
轴上一点,过圆心 作直线
作直线 的垂线交椭圆右准线于点
的垂线交椭圆右准线于点 .问:直线
.问:直线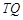 能否与圆
能否与圆 总相切,如果能,求出点
总相切,如果能,求出点 的坐标;如果不能,说明理由.
的坐标;如果不能,说明理由.
(理)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数 是
是 图像上的两点,横坐标为
图像上的两点,横坐标为 的点
的点 满足
满足 (
( 为坐标原点).
为坐标原点).
(1)求证: 为定值;
为定值;
(2)若
 ,
,
求 的
的 值;
值;
(3)在(2)的条件下,若
 ,
, 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 都成立,试求实数
都成立,试求实数 的取值范围.
的取值范围.
本题共有3个小题 ,第1小题满分4分,第2小题满分6分、第3小题满分6分.
,第1小题满分4分,第2小题满分6分、第3小题满分6分.
设 ,常数
,常数 ,定义运算“
,定义运算“ ”:
”: ,定义运算“
,定义运算“ ”:
”: ;对于两点
;对于两点 、
、 ,定义
,定义 .
.
(1)若 ,求动点
,求动点 的轨迹
的轨迹 ;
;
(2)已知直线 与(1)中轨迹
与(1)中轨迹 交于
交于 、
、 两点,若
两点,若 ,试求
,试求
 的值;
的值;
(3)在(2)中条件下,若直线 不过原点且与
不过原点且与 轴交于点S,与
轴交于点S,与 轴交于点T,并且与(1)中轨迹
轴交于点T,并且与(1)中轨迹 交于不同两点P、Q , 试求
交于不同两点P、Q , 试求 的取值范围.
的取值范围.
本题共有2个小题,第 1小题满分6分,第2小题满分10分.
1小题满分6分,第2小题满分10分.
某火山喷发停止后,为测量的需要,设距离喷口中心 米内的圆环面为第
米内的圆环面为第 区、
区、 米至
米至 米的圆环面为第
米的圆环面为第 区、……、第
区、……、第 米至
米至 米的圆环面为
米的圆环面为 第
第 区,…,现测得第
区,…,现测得第 区火山灰平均每平方米为1000千克、第
区火山灰平均每平方米为1000千克、第 区每平方米的平均重量较第
区每平方米的平均重量较第 区减少
区减少 、第
、第 区较第
区较第 区又减少
区又减少
 ,以此类推,求:
,以此类推,求:
(1)离火山口1225米处的圆环面平均每平方米火山灰重量(结果精确到1千克)?
(2)第几区内的火 山灰总重量最大?
山灰总重量最大?
本题共有2个小题,每小题满分各7分.
如图,在四棱锥 中,底面为直角梯形,
中,底面为直角梯形, ,
, 垂直于底面
垂直于底面 ,
, ,
, 分别为
分别为 的中点.
的中点.
(1)求证: ;
;
(2)求 与平面
与平面 所成的角.
所成的角.
本题共有2个小题,第1小题满分8分,第2小题满分6分.
已知函数 ,
,  .
.
(1)若 ,求函数
,求函数 的值;
的值;
(2)求函数 的值域.
的值域.