扇形AOB的周长为8 cm.
(1)若这个扇形的面积为3 cm2,求圆心角的大小;
(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB.
已知f(x)是实数集R上的函数,且对任意x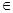 R,f(x)=f(x+1)+f(x-1)恒成立.
R,f(x)=f(x+1)+f(x-1)恒成立.
(1)求证:f(x)是周期函数.
(2)已知f(-4)=2,求f(2012).
盒子内有大小相同的9个球,其中2个红色小球,3个白色小球,4个黑色小球,规定取出1红色小球得到1分, 取出1白色小球得到0分, 取出1个黑色小球得到-1分,现从盒子中任取3个小球。
(1)求取出的3个球颜色互不相同的概率;
(2)求取出的3个球得分之和恰好为1分的概率;
(3)设ξ为取出的3个球中白色球的个数,求ξ的分布列及数学期望.
已知等比数列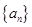 中,
中,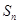 为前
为前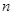 项和且
项和且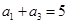 ,
,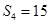 ,
,
(1)求数列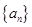 的通项公式。
的通项公式。
(2)设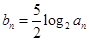 ,求
,求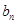 的前
的前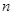 项和
项和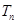 的值。
的值。
已知函数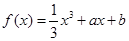 ,
,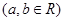 在
在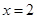 处取得极小值
处取得极小值 。求a+b的值
。求a+b的值
已知函数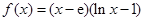
 为自然对数的底数).
为自然对数的底数).
(1)求曲线 在
在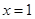 处的切线方程;
处的切线方程;
(2)若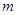 是
是 的一个极值点,且点
的一个极值点,且点 ,
,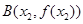 满足条件:
满足条件: .
.
(ⅰ)求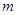 的值;
的值;
(ⅱ)若点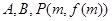 是三个不同的点, 判断
是三个不同的点, 判断 三点是否可以构成直角三
三点是否可以构成直角三
角形?请说明理由。