设f(x)是定义在区间(1，＋∞)上的函数，其导函数为f′(x)．如果存在实数a和函数h(x)，其中h(x)对任意的x∈(1，＋∞)都有h(x)＞0，使得f′(x)＝h(x)(x2－ax＋1)，则称函数f(x)具有性质P(a)．
(1)设函数f(x)＝ln x＋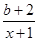
(x＞1)，其中b为实数．
①求证：函数f(x)具有性质P(b)；
②求函数f(x)的单调区间；
(2)已知函数g(x)具有性质P(2)．给定x1，x2∈(1，＋∞)，x1＜x2，设m为实数，α＝mx1＋(1－m)x2，β＝(1－m)x1＋mx2，且α＞1，β＞1，若|g(α)－g(β)|＜|g(x1)－g(x2)|，求m的取值范围．
A是△BCD平面外的一点，E，F分别是BC，AD的中点．
(1)求证：直线EF与BD是异面直线；
(2)若AC⊥BD，AC＝BD，求EF与BD所成的角．
如图所示，在边长为5＋
的长方形ABCD中，以A为圆心画一个扇形，以O为圆心画一个圆，M，N，K为切点，以扇形为圆锥的侧面，以圆O为圆锥底面，围成一个圆锥，求圆锥的全面积与体积．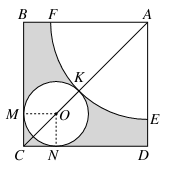
一个多面体的直观图及三视图如图所示：(其中M、N分别是AF、BC的中点)
(1)求证：MN∥平面CDEF；
(2)求多面体A－CDEF的体积．
已知正三棱锥V－ABC的正视图、侧视图和俯视图如图所示．
(1)画出该三棱锥的直观图；
(2)求出侧视图的面积．
已知某几何体的俯视图是如图所示的矩形，正视图是一个底边长为8，高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6，高为4的等腰三角形．
(1)求该几何体的体积V；
(2)求该几何体的侧面积S．