记函数fn(x)=a·xn-1(a∈R,n∈N*)的导函数为f′n(x),已知f′3(2)=12.
(1)求a的值;
(2)设函数gn(x)=fn(x)-n2ln x,试问:是否存在正整数n使得函数gn(x)有且只有一个零点?若存在,请求出所有n的值;若不存在,请说明理由;
(3)若实数x0和m(m>0且m≠1)满足 =
=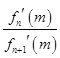 ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.
(本小题满分12分)已知函数 (
( ).
). 若函数
若函数 在
在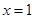 处取得极值,求
处取得极值,求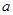 的值;
的值;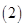 在
在 的条件下,求证:
的条件下,求证: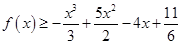 ;
;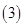 当
当 时,
时,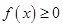 恒成立,求
恒成立,求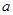 的取值范围.
的取值范围.
(本小题满分12分)在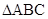 中,顶点
中,顶点 ,
, ,
, 、
、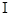 分别是
分别是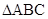 的重心和内心,且
的重心和内心,且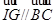 .
. 求顶点
求顶点 的轨迹
的轨迹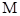 的方程;
的方程; 过点
过点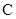 的直线交曲线
的直线交曲线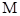 于
于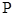 、
、 两点,
两点,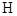 是直线
是直线 上一点,设直线
上一点,设直线 、
、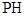 、
、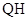 的斜率分别为
的斜率分别为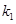 ,
,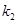 ,
,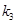 ,求证:
,求证: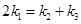 .
.
(本小题满分12分)如图,在四棱锥 中,
中,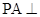 平面
平面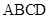 ,
, ,四边形
,四边形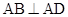 ,
,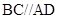 且
且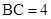 ,点
,点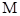 为
为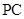 中点.
中点.
 求证:平面
求证:平面 平面
平面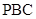 ;
; 求点
求点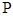 到平面
到平面 的距离.
的距离.
(本小题满分12分)根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如下图显示.
 已知
已知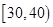 、
、 、
、 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求 ,
, 的值;
的值; 该电子商务平台将年龄在
该电子商务平台将年龄在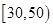 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,并在这5人中随机抽取3人进行回访,求此三人获得代金券总和为200元的概率.
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,并在这5人中随机抽取3人进行回访,求此三人获得代金券总和为200元的概率.
(本小题满分12分)在 中,
中, ,
, .
. 求角
求角 的值;
的值; 设
设 ,求
,求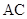 .
.