设直线 与直线
与直线 交于
交于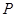 点.
点.
(1)当直线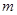 过
过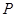 点,且与直线
点,且与直线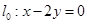 垂直时,求直线
垂直时,求直线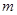 的方程;
的方程;
(2)当直线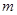 过
过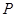 点,且坐标原点
点,且坐标原点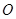 到直线
到直线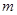 的距离为
的距离为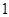 时,求直线
时,求直线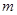 的方程.
的方程.
设p:实数x满足 <0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且
<0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且 p是
p是 q的必要不充分条件,求a的取值范围.
q的必要不充分条件,求a的取值范围.
已知椭圆C的中心在原点,焦点y在轴上,焦距为 ,且过点M
,且过点M .
.
(1)求椭圆C的方程;
(2)若过点 的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由.
的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由.
如图,在四棱柱 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,
, ,
, 是线段
是线段 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)若 平面
平面 且
且 ,求平面
,求平面 和平面
和平面 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
设数列{an}前n项和为Sn,点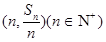 均在直线
均在直线 上.
上.
(1)求数列{an}的通项公式;
(2)设 ,Tn是数列{bn}的前n项和,试求Tn;
,Tn是数列{bn}的前n项和,试求Tn;
(3)设cn=anbn,Rn是数列{cn}的前n项和,试求Rn.