如图,有一块正方形区域ABCD,现在要划出一个直角三角形AEF区域进行绿化,满足:EF=1米,设角AEF=θ,θ ,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.
,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.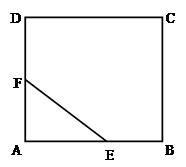
(1)求总费用y关于θ的函数.
(2)求最小的总费用和对应θ的值.
(本小题满分17分)某地政府招商引资,为吸引外商,决定第一年产品免税.某外资厂该年 型产品出厂价为每件
型产品出厂价为每件 元,年销售量为
元,年销售量为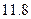 万件,第二年,当地政府开始对该商品征收税率为
万件,第二年,当地政府开始对该商品征收税率为 ,即销售
,即销售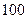 元要征收
元要征收 元)的税收,于是该产品的出厂价上升为每件
元)的税收,于是该产品的出厂价上升为每件 元,预计年销售量将减少
元,预计年销售量将减少 万件.
万件.
(1) 将第二年政府对该商品征收的税收 (万元)表示成
(万元)表示成 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
(2) 要使第二年该厂的税收不少于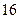 万元,则税率
万元,则税率 的范围是多少?
的范围是多少?
(3) 在第二年该厂的税收不少于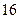 万元的前提下,要让厂家获得最大销售金额,则
万元的前提下,要让厂家获得最大销售金额,则 应为多少?
应为多少?
(本小题满分16分)已知两定点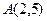 ,
,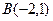 ,
,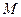 (在第一象限)和
(在第一象限)和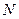 是过原点的直线
是过原点的直线 上的两个动点,且
上的两个动点,且 ,
, ∥
∥ ,如果直线
,如果直线 和
和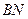 的交点
的交点 在
在 轴上,求点
轴上,求点 的坐标.
的坐标.
(本小题满分15分)已知向量 ,
, ,
, .
.
(1)若点 、
、 、
、 能构成三角形,求实数
能构成三角形,求实数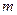 应满足的条件;
应满足的条件;
(2)若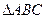 为直角三角形,且
为直角三角形,且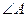 为直角,求实数
为直角,求实数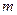 的值.
的值.
(本小题满分15分)已知函数

 的图象如图所示.
的图象如图所示.
(1)求函数 的解析式;
的解析式;
(2)令 ,求
,求 的最大值.
的最大值.
已知函数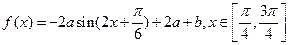 是否存在常数
是否存在常数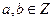 ,使得
,使得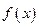 的值域为
的值域为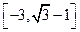 。若存在,求出a,b的值;若不存在,请说明理由。
。若存在,求出a,b的值;若不存在,请说明理由。