某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示：
| |
积极参加班级工作 |
不太主动参加班级工作 |
合计 |
| 学习积极性高 |
18 |
7 |
25 |
| 学习积极性一般 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少？抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少？
(2)试运用独立性检验的思想方法点拨：学生的学习积极性与对待班级工作的态度是否有关系？并说明理由．(参考下表)
| P(K2≥k) |
0．50 |
0．40 |
0．25 |
0．15 |
0．10 |
0．05 |
0．025 |
0．010 |
0．005 |
0．001 |
| k |
0．455 |
0．708 |
1．323 |
2．072 |
2．706 |
3．841 |
5．024 |
6．635 |
7．879 |
10．828 |
（本小题满分14分）
已知f(x)＝x2＋bx＋c为偶函数，曲线y＝f(x)过点(2,5)，g(x)＝(x＋a)f(x)．
(1)求f(x)的解析式；
(2)若曲线y＝g(x)有斜率为0的切线，求实数a的取值范围；
(3)若当x＝1时，函数y＝g(x)取得极值，确定y＝g(x)的单调区间．
（本小题满分13分）
已知双曲线C: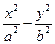
=1(a>0,b>0)的离心率为
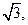焦点到渐近线的距离为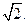
(1)求双曲线C的方程;
(2)已知直线x-y+m
=0与双曲线C交于不同的两点A,B,且线段AB的中点在抛物
线y2="4" x上,求m的值.
（本小题满分12分）
已知函数f(x)＝－x3＋x2＋ax＋b(a，b∈R)．
(1)若a＝3，试确定函数f(x)的单调区间；
(2)若函数f(x)在其图象上任意一点(x0，f(x0))处切线的斜率都小于2a2，求a的取值范围．
(本小题满分12分)已知命题p:函数f(x)=loga|x|在(0,+∞)上单调递增,命题q:关于x的方程x2+2x+loga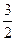
=0的解集只有一个子集,p∨q为真,(¬p)∨(¬q)也为真,求实数a的取值范围.
(本小题满分12分)
已知f(x)、g(x)分别为奇函数、偶函数，且f(x)＋g(x)＝2x+2x，求f(x)、g(x)的解析式．