经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量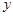 (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度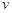 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为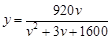 (
(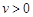 ).
).
(1)在该时段内,当汽车的平均速度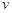 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
(2)若要求在该时段内车流量超过 千辆/时,则汽车的平均速度应在什么范围内?
千辆/时,则汽车的平均速度应在什么范围内?
(选修4—4:坐标系与参数方程)若两条曲线的极坐标方程分别为 =l与
=l与 =2cos(θ+)们相交于A,B两点,求线段AB的长。
=2cos(θ+)们相交于A,B两点,求线段AB的长。
(选修4—1:几何证明选讲)已知:如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=2 ,求EF的长。
,求EF的长。
(本小题满分12分)设 ,其中
,其中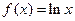 ,且
,且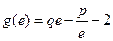 (
(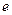 为自然对数的底)
为自然对数的底)
(1)求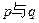 的关系;
的关系;
(2)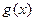 在其定义域内的单调函数,求
在其定义域内的单调函数,求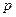 的取值范围;
的取值范围;
(3)求证:(i)
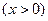
(ii)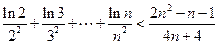 (
(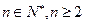 )。
)。
(本小题满分12分)函数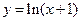
(1)若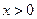 ,证明
,证明 ;
;
(2)若不等式 时
时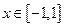 和
和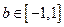 都恒成立,求实数
都恒成立,求实数 的取值范围。
的取值范围。
(本小题满分12分)已知函数 ,将
,将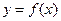 的图象向左平移两个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数
的图象向左平移两个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数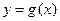 的图象,
的图象,
(1)求函数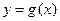 ;(2)求函数
;(2)求函数 的最大值。
的最大值。