为喜迎马年新春佳节,某商场在正月初六进行抽奖促销活动,当日在该店消费满500元的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有 “马”“上”“有”“钱”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“钱”字球,则停止取球.获奖规则如下:依次取到标有“马”“上”“有”“钱”字的球为一等奖;不分顺序取到标有“马”“上”“有”“钱”字的球,为二等奖;取到的4个球中有标有“马”“上”“有”三个字的球为三等奖.
(1)求分别获得一、二、三等奖的概率;
(2)设摸球次数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分14分)
如图,已知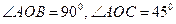 ,
,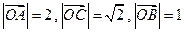 .
.
(1)试用向量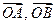 来表示向量
来表示向量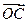 ;
;
(2)若向量 ,
,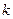
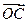 的终点在一条直线上,
的终点在一条直线上,
求实数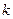 的值;
的值;
(3 )设
)设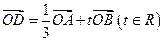 ,当
,当 、
、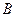 、
、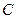 、
、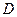 四点共圆时, 求
四点共圆时, 求 的值.
的值.
 |
( 本小题满分13分)
本小题满分13分)
从某校高一年级参加期末考试的学生中抽出 名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(1)根据频率分布直方图估计这次考试该年级的数学平均分;
(2) 已知在[90,100]内的学生的数学成绩都不相同,且都在95分以上(不含95分),现用简单随机抽样方法,从 这
这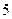 个数中任取
个数中任取 个数,求这
个数,求这 个数恰好是两名学生的数学成绩的概率.
个数恰好是两名学生的数学成绩的概率.
 |
(本小题满分13分)
已知向量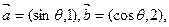 满足
满足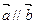 ,其中
,其中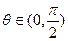 .
.
(1)求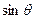 和
和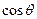 的值;
的值;
(2)若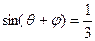 ,求
,求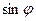 的值.
的值.
(本小题满分13分)
已知函数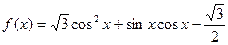 .
.
(1)求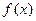 的单调递增区间;
的单调递增区间;
(2)函数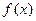 的图象经过怎样的平移可使其对应的函数成为偶函数? 请写出一种正确的平移方法,并说明理由.
的图象经过怎样的平移可使其对应的函数成为偶函数? 请写出一种正确的平移方法,并说明理由.
(本小题满分13分)
某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 |
A |
B |
C |
D |
E E |
销售额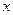 (千万元) (千万元) |
3 |
5 |
6 |
7 |
9 9 |
利润额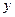 (百万元) (百万元) |
2 |
3 |
3 |
4 |
5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的 相关关系;
相关关系;
(2)用最小二乘法计算利润额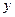 关于销售额
关于销售额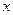 的回归直线方程;
的回归直线方程;
(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).