希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)
| |
1号 |
2号 |
3号 |
4号 |
5号 |
总数 |
| 甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
| 乙班 |
89 |
100 |
95 |
119 |
97 |
500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)求两班比赛数据的中位数;
(2)计算两班比赛数据的方差,并比较哪一个小;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.
九年级学生体育模考成绩统计表
| 体育成绩 |
人数(人) |
百分比(%) |
| 26 |
||
| 27 |
m |
|
| 28 |
8 |
16 |
| 29 |
24 |
|
| 30 |
15 |

根据上面提供的信息,回答下列问题:
(1)m=;抽取的部分学生体育模考成绩的中位数为;
(2)已知该校九年级共有500名学生,如果体育模考成绩达29分(含29分)为优秀,请估计该校九年级学生体育模考成绩达到优秀的总人数.
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)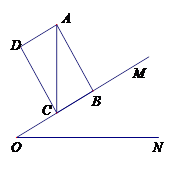
(本题满分8分,每题4分)
(1)解方程: x2-4x-3=0(2)解不等式组: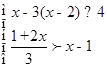
(本题满分8分,每题4分)计算:
(1)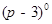 +2sin45°-
+2sin45°-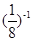
(2)2(a+1)-(3-a)(3+a)-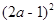
(本题12分) 如图,已知直线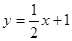 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点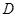 ,抛物线
,抛物线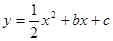 与直线交于
与直线交于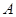 、
、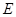 两点,与
两点,与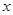 轴交于
轴交于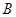 、
、 两点,且
两点,且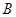 点坐标为(1,0).
点坐标为(1,0).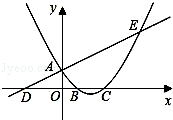
(1)求该抛物线的解析式;
(2)动点 在
在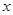 轴上移动,当△
轴上移动,当△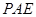 是直角三角形时,直接写出点
是直角三角形时,直接写出点 的坐标;
的坐标;
(3)在抛物线的对称轴上找一点 ,使|
,使|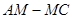 |的值最大,求出点
|的值最大,求出点 的坐标.
的坐标.