已知,在如图所示的“风筝”图案中, , , .求证: .

解不等式 .
已知抛物线 的对称轴是直线 ,与 轴相交于 , 两点(点 在点 右侧),与 轴交于点 .

(1)求抛物线的解析式和 , 两点的坐标;
(2)如图1,若点 是抛物线上 、 两点之间的一个动点(不与 、 重合),是否存在点 ,使四边形 的面积最大?若存在,求点 的坐标及四边形 面积的最大值;若不存在,请说明理由;
(3)如图2,若点 是抛物线上任意一点,过点 作 轴的平行线,交直线 于点 ,当 时,求点 的坐标.
在 中, , , 于点 .
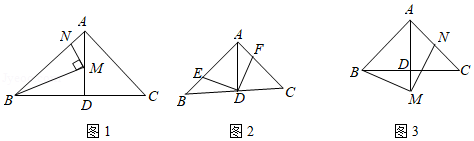
(1)如图1,点 , 分别在 , 上,且 ,当 , 时,求线段 的长;
(2)如图2,点 , 分别在 , 上,且 ,求证: ;
(3)如图3,点 在 的延长线上,点 在 上,且 ,求证: .
如图,在 中, ,以 为直径作 ,点 为 上一点,且 ,连接 并延长交 的延长线于点 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求圆的半径及 的长.
