已知抛物线的对称轴是直线,与轴相交于,两点(点在点右侧),与轴交于点.

(1)求抛物线的解析式和,两点的坐标;
(2)如图1,若点是抛物线上、两点之间的一个动点(不与、重合),是否存在点,使四边形的面积最大?若存在,求点的坐标及四边形面积的最大值;若不存在,请说明理由;
(3)如图2,若点是抛物线上任意一点,过点作轴的平行线,交直线于点,当时,求点的坐标.
已知:甲、乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到B地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)求甲车离出发地的距离
 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;(2)当它们行驶到与各自出发地的距离相等时,用了
 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;(3)在(2)的条件下,求
 它们在行驶的过程中相遇的时间.
它们在行驶的过程中相遇的时间.
在边长为1的正方形网格中,有形如帆船的图案①和半径为2的⊙P.
 |
⑴将图案①进行平移,使A点平移到点E,画出平移后的图案;
⑵以点M为位似中心,在网格中将图案①放大2倍,画出放大后的图案
 ,并在放大后的图案中标出线段AB的对应线段CD;
,并在放大后的图案中标出线段AB的对应线段CD;⑶在⑵所画的图案中,线段CD被⊙P所截得的弦长为▲(结果保留根号).
有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).小明将这4张纸牌背面朝上洗匀后摸出一张,将剩余3张洗匀后再摸出一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用A,B,C,D表示);
(2)求摸出的两张牌面图形既是轴对称图形又是中心对称图形纸牌的概率.
某文具店王经理统计了2009年1月至4月A、B、C这三种型号的钢笔平均每月的销售量,并绘制图1(不完整),销售这三种型号钢笔平均每月获得的 总利润为600元,每种型号钢笔获得的利润分布情况如图2.已知C型号钢笔每支的利润是1.2元,请你结合图中的信息,解答下列问题:
总利润为600元,每种型号钢笔获得的利润分布情况如图2.已知C型号钢笔每支的利润是1.2元,请你结合图中的信息,解答下列问题:
(1)销售B型号钢笔平均每月获得的利润占总利润的▲%,A型号钢笔每支的利润是▲,B型号钢笔每支的利润是▲,C
 种型号钢笔平均每月的销售量是▲支,并将图1补充完整;
种型号钢笔平均每月的销售量是▲支,并将图1补充完整;(2)王经理计划5月份购进A、B、C这三种型号钢笔共900支,请你结合1月至4月平均每月的销售情况(不考虑其它因素),设计一个方案,使获得的利润最大,并说明理由.
如图,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE 交BC于E, EC=AB, F、G分别是AB、AD的中点.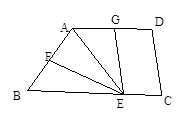
求证:(1)△AGE≌AFE;
(2)EF=CD.