已知函数f(x)=cos2ωx+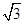 sinωxcosωx-
sinωxcosωx-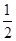 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω值及f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=1,b=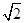 ,f(
,f(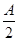 )=
)=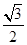 ,求角C的大小.
,求角C的大小.
如图,在四棱锥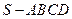 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,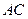 与
与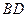 的交点为O.
的交点为O.
(Ⅰ)求证: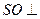 平面
平面 ;
;
(Ⅱ)已知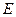 为侧棱
为侧棱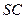 上一个动点. 试问对于
上一个动点. 试问对于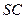 上任意一点
上任意一点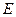 ,平面
,平面 与平面
与平面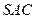 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.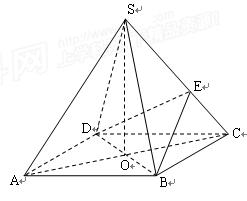
(本题满分1 3分)
3分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
| 环数 |
7 |
8 |
9 |
10 |
| 命中次数 |
2 |
7 |
8 |
3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为 次、
次、 次,每个基本事件为(m,n).
次,每个基本事件为(m,n).
求“ ”的概率.
”的概率.
设函数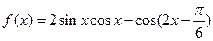 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当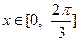 时,求函数
时,求函数 的最大值及取得最大值时的
的最大值及取得最大值时的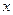 的值.
的值.
已知椭圆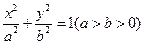 经过点
经过点 ,过右焦点F且不与x轴重合的动直线L交椭圆于
,过右焦点F且不与x轴重合的动直线L交椭圆于 两点,当动直线L的斜率为2时,坐标原点O到L的距离为
两点,当动直线L的斜率为2时,坐标原点O到L的距离为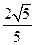 .
.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 过F的另一直线交椭圆于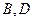 两点,且
两点,且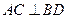 ,当四边形
,当四边形 的面积S=
的面积S=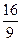 时,求直线L的方程.
时,求直线L的方程.
已知函数f(x)= 在x=-2处有极值.
在x=-2处有极值.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在区间[-3,3]上有且仅有一个零点,求b的取值范围.