某厂生产某种产品的年固定成本为250万元,每生产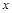 万件,需另投入的成本为
万件,需另投入的成本为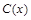 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时,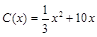 ;当年产量不小于80万件时,
;当年产量不小于80万件时,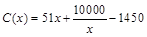 .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
(1)写出年利润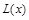 (万元)关于年产量
(万元)关于年产量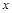 (万件)的函数关系式;
(万件)的函数关系式;
(2)年产量为多少万件时,该厂在该产品的生产中所获利润最大?最大利润是多少?
已知向量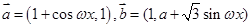 (
( 为常数且
为常数且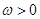 ),函数
),函数 在
在 上的最大值为
上的最大值为 .
.
(1)求实数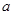 的值;
的值;
(2)把函数 的图象向右平移
的图象向右平移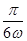 个单位,可得函数
个单位,可得函数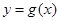 的图象,若
的图象,若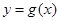 在
在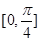 上为增函数,求
上为增函数,求 取最大值时的单调增区间.
取最大值时的单调增区间.
等比数列 中,已知
中,已知 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若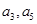 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 的通项公式及前
的通项公式及前 项和
项和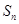 。
。
已知函数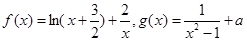
(1)求函数 的单调区间.
的单调区间.
(2)若方程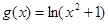 有4个不同的实根,求
有4个不同的实根,求 的范围?
的范围?
(3)是否存在正数 ,使得关于
,使得关于 的方程
的方程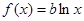 有两个不相等的实根?如果存在,求b
有两个不相等的实根?如果存在,求b 满足的条件,如果不存在,说明理由.
满足的条件,如果不存在,说明理由.
已知椭圆C: (
(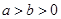 )的短轴长为2,离心率为
)的短轴长为2,离心率为
(1)求椭圆C的方程
(2)若过点M(2,0)的引斜率为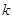 的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足
的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足 (
(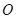 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数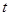 的取值范围?
的取值范围?
某种食品是经过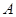 、
、 、
、 三道工序加工而成的,
三道工序加工而成的,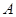 、
、 、
、 工序的产品合格率分别为
工序的产品合格率分别为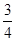 、
、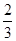 、
、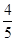 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
(1)正式生产前先试生产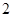 袋食品,求这2袋食品都为废品的概率;
袋食品,求这2袋食品都为废品的概率;
(2)设 为加工工序中产品合格的次数,求
为加工工序中产品合格的次数,求 的分布列和数学期望.
的分布列和数学期望.