(本小题满分12分)
已知向量
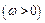 ,函数
,函数 ,且
,且 图
图 象上一个最高点的坐标为
象上一个最高点的坐标为 ,与之相邻
,与之相邻 的一个最低点的坐标为
的一个最低点的坐标为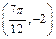 .
.
(1)求 的解析式;
的解析式;
(2)在△ABC中, 是角A、B、C所对的边,且满足
是角A、B、C所对的边,且满足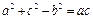 ,求角B的大
,求角B的大
小以及 的取值范围.
的取值范围.
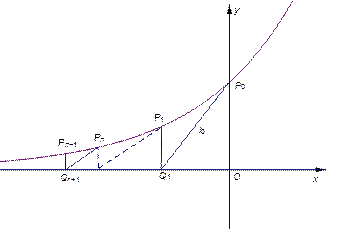
如图,过曲线 :
: 上一点
上一点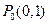 作曲线
作曲线 的切线
的切线 交
交 轴于点
轴于点 ,又过
,又过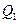 作
作  轴的垂线交曲线
轴的垂线交曲线 于点
于点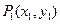 ,然后再过
,然后再过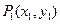 作曲线
作曲线 的切线
的切线 交
交 轴于点
轴于点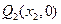 ,又过
,又过 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,
,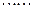 ,以此类推,过点
,以此类推,过点 的切线
的切线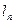 与
与 轴相交于点
轴相交于点 ,再过点
,再过点 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 (
( N
N ).
).
(1) 求 、
、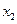 及数列
及数列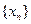 的通项公式;
的通项公式;
(2) 设曲线 与切线
与切线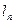 及直线
及直线 所围成的图形面积为
所围成的图形面积为 ,求
,求 的表达式;
的表达式;
(3) 在满足(2)的条件下, 若数列 的前
的前 项和为
项和为 ,求证:
,求证:
 N
N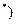 .
.
(本小题满分14分)
设函数 在
在 上的导函数为
上的导函数为 ,
, 在
在 上的导函数为
上的导函数为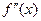 ,若在
,若在 上,
上,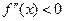 恒成立,则称函数
恒成立,则称函数 在
在 上为“凸函数”.已知
上为“凸函数”.已知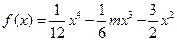 .
.
(1)若 为区间
为区间 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数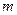 的值;
的值;
(2)若当实数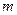 满足
满足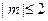 时,函数
时,函数 在
在 上总为“凸函数”,求
上总为“凸函数”,求 的最大值.
的最大值.
(本小题满分14分)
已知椭圆 的离心率
的离心率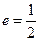 . 直线
. 直线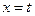 (
( )与曲线
)与曲线 交于不同的两点
交于不同的两点 ,以线段
,以线段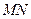 为直径作圆
为直径作圆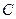 ,圆心为
,圆心为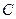 .
.
(1) 求椭圆 的方程;
的方程;
(2) 若圆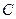 与
与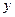 轴相交于不同的两点
轴相交于不同的两点 ,求
,求 的面积的最大值.
的面积的最大值.
(本小题满分l4分)
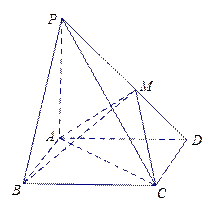
如图4,在四棱锥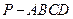 中,底面
中,底面 是矩形,
是矩形,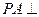 平面
平面 ,
, ,
, ,
, 于点
于点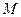 .
.
(1) 求证:
 ;
;
(2) 求直线 与平面
与平面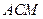 所成的角的余弦值.
所成的角的余弦值.