(本小题满分14分)
设函数 在
在 上的导函数为
上的导函数为 ,
, 在
在 上的导函数为
上的导函数为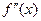 ,若在
,若在 上,
上,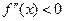 恒成立,则称函数
恒成立,则称函数 在
在 上为“凸函数”.已知
上为“凸函数”.已知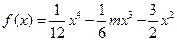 .
.
(1)若 为区间
为区间 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数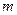 的值;
的值;
(2)若当实数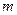 满足
满足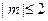 时,函数
时,函数 在
在 上总为“凸函数”,求
上总为“凸函数”,求 的最大值.
的最大值.
椭圆 的离心率为
的离心率为 ,长轴端点A与短轴端点B间的距离为
,长轴端点A与短轴端点B间的距离为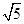 .(1)求椭圆
.(1)求椭圆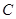 的方程;
的方程;
(2)P为椭圆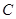 上一动点,求
上一动点,求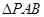 的面积的最大值。
的面积的最大值。
在平面直角坐标系中,以坐标原点为极点, 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为 ,直线L的直角坐标方程为
,直线L的直角坐标方程为 ,且点A在直线L上.
,且点A在直线L上.
(1)求 的值;
的值;
(2)圆C的参数方程为 ,(
,(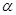 为参数),试判断直线L与圆C的位置关系并说明理由.
为参数),试判断直线L与圆C的位置关系并说明理由.
已知函数 且此函数图象过点(1,5).
且此函数图象过点(1,5).
(1)求实数m的值;
(2)判断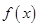 在
在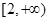 上的单调性,并证明你的结论。
上的单调性,并证明你的结论。
命题 :
: 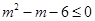 ;命题
;命题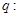 不等式
不等式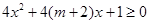 对
对 恒成立。如果命题
恒成立。如果命题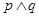 为真,求实数
为真,求实数 的取值范围.
的取值范围.
某校高二年级的一次数学考试中,为了分析学生的得分情况,随机抽取 名同学的成绩,数据的分组统计表如下:
名同学的成绩,数据的分组统计表如下:
| 分组 |
频数 |
频率 |
频率/组距 |
| (40,50] |
2 |
0.02 |
0.002 |
| (50,60] |
4 |
0.04 |
0.004 |
| (60,70] |
11 |
0.11 |
0.011 |
| (70,80] |
38 |
0.38 |
0.038 |
| (80,90] |
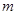 |
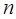 |
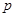 |
| (90,100] |
11 |
0.11 |
0.011 |
| 合计 |
 |
 |
 |
(1)求出表中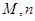 的值;
的值;
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在 中的6位同学中任意抽取2人进行调查,求分数在
中的6位同学中任意抽取2人进行调查,求分数在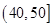 和
和 中各有一人的概率.
中各有一人的概率.