在平面直角坐标系中,以坐标原点为极点, 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为 ,直线L的直角坐标方程为
,直线L的直角坐标方程为 ,且点A在直线L上.
,且点A在直线L上.
(1)求 的值;
的值;
(2)圆C的参数方程为 ,(
,(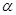 为参数),试判断直线L与圆C的位置关系并说明理由.
为参数),试判断直线L与圆C的位置关系并说明理由.
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3题,每人答对其中2题就停止答题,即闯关成功.已知在6道被选题中,甲能答对其中的4道题,乙答对每道题的概率都是.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为ξ,求ξ的分布列.
袋中共有10个大小相同的编号为1,2,3的球,其中1号球有1个,2号球有m个,3号球有n个.从袋中依次摸出2个球,已知在第一次摸出3号球的前提下,再摸出一个2号球的概率是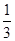 .
.
(1)求m,n的值;
(2)从袋中任意摸出2个球,设得到小球的编号数之和为ξ,求随机变量ξ的分布列.
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列.
在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有6人.
(1)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现从中随机抽取2人上台抽奖,求a和b至少有一人上台抽奖的概率;
(2)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖.求该代表中奖的概率.