某校高二年级的一次数学考试中,为了分析学生的得分情况,随机抽取 名同学的成绩,数据的分组统计表如下:
名同学的成绩,数据的分组统计表如下:
| 分组 |
频数 |
频率 |
频率/组距 |
| (40,50] |
2 |
0.02 |
0.002 |
| (50,60] |
4 |
0.04 |
0.004 |
| (60,70] |
11 |
0.11 |
0.011 |
| (70,80] |
38 |
0.38 |
0.038 |
| (80,90] |
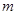 |
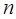 |
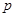 |
| (90,100] |
11 |
0.11 |
0.011 |
| 合计 |
 |
 |
 |
(1)求出表中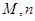 的值;
的值;
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在 中的6位同学中任意抽取2人进行调查,求分数在
中的6位同学中任意抽取2人进行调查,求分数在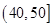 和
和 中各有一人的概率.
中各有一人的概率.
已知函数 。
。
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)若 ,证明当
,证明当 时,函数
时,函数 的图象恒在函数
的图象恒在函数 图象的上方.
图象的上方.
某幼儿园在“六·一儿童节”开展了一次亲子活动,此次活动由宝宝和父母之一(后面以家长代称)共同完成,幼儿园提供了两种游戏方案:
方案一宝宝和家长同时各抛掷一枚质地均匀的正方体骰子(六个面的点数分别是1,2,3,4,5,6),宝宝所得点数记为 ,家长所得点数记为
,家长所得点数记为 ;
;
方案二宝宝和家长同时按下自己手中一个计算器的按钮(此计算器只能产生区间[1,6]的随机实数),宝宝的计算器产生的随机实数记为 ,家长的计算器产生的随机实数记为
,家长的计算器产生的随机实数记为 .
.
(Ⅰ)在方案一中,若 ,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
(Ⅱ)在方案二中,若 ,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
设数列 的前
的前 项和为
项和为 ,且
,且 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知函数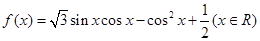 .
.
(1)求函数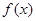 的最小正周期;
的最小正周期;
(2)求函数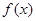 在区间
在区间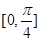 上的函数值的取值范围.
上的函数值的取值范围.
已知椭圆 过点
过点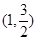 ,且离心率
,且离心率 。
。
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若直线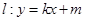 与椭圆
与椭圆 相交于
相交于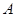 ,
,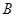 两点(
两点( 不是左右顶点),椭圆的右顶点为D,且满足
不是左右顶点),椭圆的右顶点为D,且满足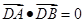 ,试判断直线
,试判断直线 是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由。
是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由。