已知实数x,y满足不等式组 ,若目标函数z=y-ax取得最大值时的唯一最优解是(1,3),求实数a的取值范围.
,若目标函数z=y-ax取得最大值时的唯一最优解是(1,3),求实数a的取值范围.
如图,四棱锥 中,
中, ,底面
,底面 为直角梯形,
为直角梯形,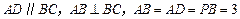 ,点
,点 在棱
在棱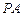 上,且
上,且 .
.
(1)求异面直线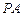 与
与 所成的角;
所成的角;
(2)求证: 平面
平面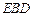 ;
;
(3)求二面角 的余弦值.
的余弦值.
已知曲线 的方程是
的方程是 .
.
(1)若曲线 是椭圆,求
是椭圆,求 的取值范围;
的取值范围;
(2)若曲线 是双曲线,且有一条渐近线的倾斜角是
是双曲线,且有一条渐近线的倾斜角是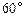 ,求此双曲线的方程.
,求此双曲线的方程.
在面积为12的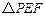 中,已知
中,已知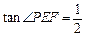 ,
,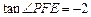 ,试建立适当的坐标系,求出分别以
,试建立适当的坐标系,求出分别以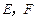 为左、右焦点且过
为左、右焦点且过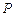 的双曲线方程.
的双曲线方程.
已知大西北某荒漠上 两点相距2千米,现准备在荒漠上围垦出一片以
两点相距2千米,现准备在荒漠上围垦出一片以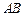 为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
(1)试求四边形另两个顶点的轨迹方程;
(2)该荒漠上有一条直线型小溪 刚好通过点
刚好通过点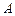 ,且
,且 与
与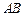 成
成 角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
已知条件 和条件
和条件 ,现在要选择适当的实数
,现在要选择适当的实数 的值,分别利用所给的两上条件作为
的值,分别利用所给的两上条件作为 构造命题:“若
构造命题:“若 则
则 ”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.