已知函数.
(1)求证:;
(2)若对恒成立,求的最大值与的最小值.
(本小题满分12分) 甲、乙、丙三人按下面的规则进行乒乓球比赛: 第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.
,且各局胜负相互独立.
求:(I)打满3局比赛还未停止的概率;
(II)比赛停止时已打局数 的分别列与期望E
的分别列与期望E .
.
(本小题满分10分) 已知 的面积为
的面积为 ,且满足
,且满足 ,设
,设 和
和 的夹角为
的夹角为

(I)求 的取值范围;
的取值范围;
(II)求函数 的最大值与最小值
的最大值与最小值
设椭圆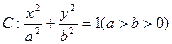 的左、右焦点分别为F1与F2,直线
的左、右焦点分别为F1与F2,直线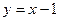 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若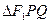 的周长为
的周长为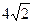 。
。
(1)求椭圆C的方程;
(2)设椭圆C经过伸缩变换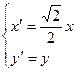 变成曲线
变成曲线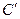 ,直线
,直线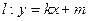 与曲线
与曲线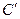 相切且与椭圆C交于不同的两点A、B,若
相切且与椭圆C交于不同的两点A、B,若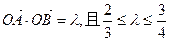 ,求
,求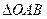 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点)
已知函数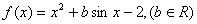 ,且对任意
,且对任意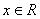 ,有
,有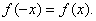
(1)求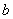 。
。
(2)已知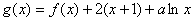 在区间(0,1)上为单调函数,求实数
在区间(0,1)上为单调函数,求实数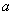 的取值范围。
的取值范围。
(3)讨论函数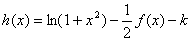 的零点个数?
的零点个数?
为加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车,每更换一辆新车,则淘汰一辆旧车,替换车为电力型和混合动力型车,今年初投入了电力型公交车128辆,混合动力型公交车400辆;计划以后电力型车每年的投入量比上一年增加50%,混合动车型车每年比上一年多投入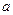 辆。
辆。
(1)求经过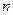 年,该市被更换的公交车总数
年,该市被更换的公交车总数 ;
;
(2)若该市计划7年内完成全部更换,求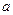 的最小值。
的最小值。