已知函数
.
(1)讨论
的单调性;
(2)设
,当
时,
,求
的最大值;
(3)已知
,估计
的近似值(精确到0.001).
(本小题满分8分)嫦娥2号月球卫星接收天线的轴
截面为如图所示的抛物线型,已知接收天线的口径(直径)
为10.8m,深度为1.2m,建立适当的坐标系,求抛物线的
标准方程和焦点坐标。
(本小题满分8分)设p :函数
:函数 在R上递增;q:方程
在R上递增;q:方程 无实根。若
无实根。若 为真,
为真, 为假,求
为假,求
 的取值范围。
的取值范围。
已知函数 .
.
(Ⅰ)判断f(x)的奇偶性,并说明理由;
(Ⅱ)若方程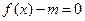 有解,求m的取值范围;
有解,求m的取值范围;
(Ⅲ)若函数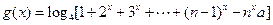 ,
, ,对任意
,对任意 都有意义,求
都有意义,求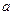 的取值范围.
的取值范围.
如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(Ⅰ)写出y关于x的函数关系式,并指出这个函数的定义域;
(Ⅱ)当AE为何值时,绿地面积最大?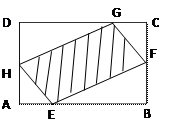
(已知函数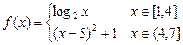 .
.
(Ⅰ)在给定的直角坐标系内画出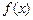 的大致图象;
的大致图象;
(Ⅱ)求函数g(x)=f(x)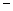
 的零点.
的零点.