设
(1)求 的单调区间;
的单调区间;
(2)求 在
在 上的最值;
上的最值;
(3)若关于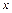 的方程
的方程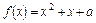 在
在 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数 的范围。
的范围。
(本小题满分12分)
已知铁矿石 和
和 的含铁率为
的含铁率为 ,冶炼每万吨铁矿石的
,冶炼每万吨铁矿石的 的排放量
的排放量 及每万吨铁矿石的价格
及每万吨铁矿石的价格 如下表:
如下表:
 |
 (万吨) (万吨) |
 (百万元) (百万元) |
|
 |
50% |
1 |
3 |
 |
70 % % |
0.5 |
6 |
某冶炼厂计划至少生产1.9万吨铁,若要求 的排放量不超过
的排放量不超过 万吨,求所需费用的最小值,并求此时铁矿石
万吨,求所需费用的最小值,并求此时铁矿石 或
或 分别购买多少万吨.
分别购买多少万吨.
(本小题满分12分)
已知正方形 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数
 图象上,且正方形的一个顶点为
图象上,且正方形的一个顶点为 .
.
(Ⅰ)试写出正方形另外三个顶点的坐标,并求 ,
, 的值;
的值;
(II)求函数的单调增区间.
(本小题满分1 2分)
2分)
解关于 的不等式
的不等式 ,其中
,其中 ,且
,且 .
.
附加题以数列 的任意相邻两项为坐标的点
的任意相邻两项为坐标的点 (
( )都在一次函数
)都在一次函数 的图象上,数列
的图象上,数列 满足
满足 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 ,
, 的前
的前 项和分别为
项和分别为 ,且
,且 ,求
,求 的值.
的值.
(12分)如图,直角三角形ABC的顶点坐标A( )、B(0,
)、B(0, ),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究
),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究 是否是定值?若是,求出定值;若不是,请说明理由.
是否是定值?若是,求出定值;若不是,请说明理由.