已知椭圆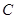 的焦点在
的焦点在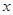 轴上,离心率
轴上,离心率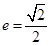 ,且经过点
,且经过点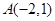 .
.
(Ⅰ)求椭圆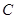 的标准方程;
的标准方程;
(Ⅱ)斜率为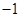 的直线
的直线 与椭圆
与椭圆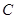 相交于
相交于 两点,求证:直线
两点,求证:直线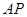 与
与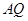 的倾斜角互补.
的倾斜角互补.
四棱锥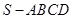 中,底面
中,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面 ,
,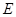 为
为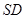 的中点,已知
的中点,已知 ,
,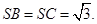

(Ⅰ)求证: ;
;
(Ⅱ)在 上求一点
上求一点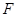 ,使
,使 平面
平面 ;
;
(Ⅲ)求三棱锥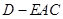 的体积.
的体积.
甲、乙两个盒子中各有3个球,其中甲盒中有2个黑球1个白球,乙盒中有1个黑球2个白球,所有球之间只有颜色区别.
(Ⅰ)若从甲、乙两个盒子中各取一个球,求取出的2个球颜色相同的概率;
(Ⅱ)将这两个盒子中的球混合在一起,从中任取2个,求取出的2个球中至少有一个黑球的概率.
设 .
.
(1)解不等式 ;
;
(2)若对任意实数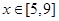 ,
, 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知极坐标系的极点为直角坐标系 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线 的极坐标方程为
的极坐标方程为 .
.
(1)求 的直角坐标方程;
的直角坐标方程;
(2)直线 (
( 为参数)与曲线C交于
为参数)与曲线C交于 ,
, 两点,与
两点,与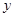 轴交于
轴交于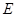 ,求
,求 的值.
的值.