如图，某一新型发电装置的发电管是横截面为矩形的水平管道，管道的长为、宽度为、高为，上下两面是绝缘板，前后两侧面、是电阻可忽略的导体板，两导体板与开关S和定值电阻相连。整个管道置于磁感应强度大小为，方向沿轴正方向的匀强磁场中。管道内始终充满电阻率为的导电液体（有大量的正、负离子），且开关闭合前后，液体在管道进、出口两端压强差的作用下，均以恒定速率v0沿x轴正向流动，液体所受的摩擦阻力不变。
（1）求开关闭合前，、两板间的电势差大小；
（2）求开关闭合前后，管道两端压强差的变化；
（3）调整矩形管道的宽和高，但保持其它量和矩形管道的横截面不变，求电阻可获得的最大功率及相应的宽高比的值。
如图所示，用跨过光滑定滑轮的缆绳将海面上一艘失去动力的小船沿直线拖向岸边．已知拖动缆绳的电动机功率恒为P，小船的质量为m，小船受到的阻力大小恒为f，经过A点时的速度大小为v0，小船从A点沿直线加速运动到B点经历时间为t1，A、B两点间距离为d，缆绳质量忽略不计．求：
(1)小船从A点运动到B点的全过程克服阻力做的功Wf；
(2)小船经过B点时的速度大小v1；
(3)小船经过B点时的加速度大小a.
一探险队员在探险时遇到一山沟，山沟的一侧竖直，另一侧的坡面呈抛物线形状．此队员从山沟的竖直一侧，以速度v0沿水平方向跳向另一侧坡面．如图所示，以沟底的O点为原点建立坐标系xOy.已知，山沟竖直一侧的高度为2h，坡面的抛物线方程为y＝
x2，探险队员的质量为m.人视为质点，忽略空气阻力，重力加速度为g.求此人落到坡面时的动能。
初速度为v0，质量为m，电荷量为+q的带电粒子逆着电场线的方向从匀强电场边缘射入匀强电场，已知射入的最大深度为d．则
(1)场强大小E=_____；
(2)带电粒子在电场区域中运动的时间 (不计带电粒子的重力)为t=______。
(15分)如图，在竖直平面内有一固定光滑轨道，其中AB是长为R的水平直轨道，BCD是圆心为O、半径为R的3/4圆弧轨道，两轨道相切与B点。在外力作用下，一小球从A点由静止开始做匀加速直线运动，到达B点时撤除外力。已知小球刚好能沿圆轨道经过最高点C，重力加速度大小为g。求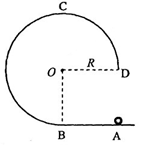
（1）小球在C点的速度的大小；
（2）小球在AB段运动的加速度的大小；
（3）小球从D点运动到A点所用的时间。
(15分)如图所示，半径R=2m的四分之一粗糙圆弧轨道AB置于竖直平面内，轨道的B端切线水平，且距水平地面高度为h=1.25m，现将一质量m=0.2kg的小滑块从A点由静止释放，滑块沿圆弧轨道运动至B点以v=5m/s的速度水平飞出(g取10m/s2)．求：
（1）小滑块沿圆弧轨道运动过程中克服摩擦力做的功；
（2）小滑块经过B点时对圆轨道的压力大小；
（3）小滑块着地时的速度大小和方向。