已知双曲线的两条渐近线分别为.
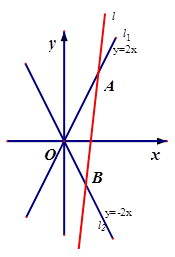
(1)求双曲线的离心率;
(2)如图,为坐标原点,动直线分别交直线于两点(分别在第一,四象限),且的面积恒为8,试探究:是否存在总与直线有且只有一个公共点的双曲线?若存在,求出双曲线的方程;若不存在,说明理由.
已知A,B 分别为曲线C: 与x轴的左、右两个交点,直线 过点B,且与 轴垂直,S为 上异于点B的一点,连结AS交曲线C于点T.
(1)若曲线C为半圆,点T为圆弧 的三等分点,试求出点S的坐标;
(2)如图,点M是以SB为直径的圆与线段TB的交点,试问:是否存在 ,使得O,M,S三点共线?若存在,求出 的值,若不存在,请说明理由。

如图,某市拟在长为的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段 ,该曲线段为函数 , 的图象,且图象的最高点为 ;赛道的后一部分为折线段 ,为保证参赛运动员的安全,限定

(Ⅰ)求A , 的值和M,P两点间的距离;
(Ⅱ)应如何设计,才能使折线段赛道 最长?
如图,四边形 是边长为 的正方形, , ,且 , 为 的中点.

(1)求异面直线NE与AM所成角的余弦值
(2)在线段AN上是否存在点S,使得 ?若存在,求线段AS的长;若不存在,请说明理由
从集合 的所有非空子集中,等可能地取出一个。
(1)记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(2)记所取出的非空子集的元素个数为 ,求 的分布列和数学期望
已知曲线 .从点 向曲线 引斜率为 的切线 ,切点为 .
(1)求数列 的通项公式;
(2)证明: