四面体
及其三视图如图所示,平行于棱
的平面分别交四面体的棱
于点
.

(1)求四面体
的体积;
(2)证明:四边形
是矩形.
设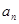 是函数
是函数
 的零点.
的零点.
(1)证明: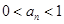 ;
;
(2)证明:
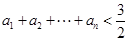 .
.
经过点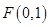 且与直线
且与直线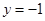 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为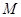 .点
.点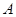 、
、 在轨迹
在轨迹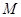 上,且关于
上,且关于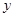 轴对称,过线段
轴对称,过线段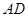 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线 ,使直线
,使直线 与轨迹
与轨迹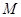 在点
在点 处的切线平行,设直线
处的切线平行,设直线 与轨迹
与轨迹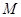 交于点
交于点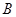 、
、 .
.
(1)求轨迹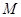 的方程;
的方程;
(2)证明: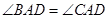 ;
;
(3)若点 到直线
到直线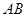 的距离等于
的距离等于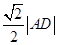 ,且△
,且△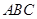 的面积为20,求直线
的面积为20,求直线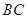 的方程.
的方程.
已知 ,设命题
,设命题 :函数
:函数 在区间
在区间 上与
上与 轴有两个不同的交点;命题
轴有两个不同的交点;命题 :
: 在区间
在区间 上有最小值.若
上有最小值.若 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.
等边三角形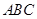 的边长为3,点
的边长为3,点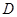 、
、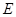 分别是边
分别是边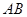 、
、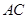 上的点,且满足
上的点,且满足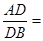
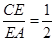 (如图1).将△
(如图1).将△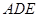 沿
沿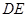 折起到△
折起到△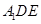 的位置,使二面角
的位置,使二面角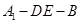 成直二面角,连结
成直二面角,连结 、
、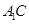 (如图2).
(如图2).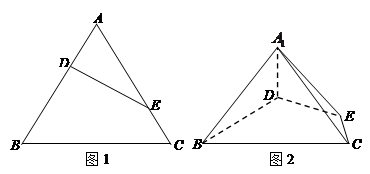
(1)求证: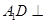 平面
平面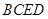 ;
;
(2)在线段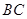 上是否存在点
上是否存在点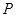 ,使直线
,使直线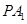 与平面
与平面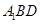 所成的角为
所成的角为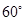 ?若存在,求出
?若存在,求出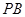 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
已知正方形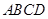 的边长为2,
的边长为2,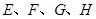 分别是边
分别是边 的中点.
的中点.
(1)在正方形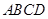 内部随机取一点
内部随机取一点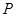 ,求满足
,求满足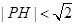 的概率;
的概率;
(2)从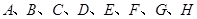 这八个点中,随机选取两个点,记这两个点之间的距离为
这八个点中,随机选取两个点,记这两个点之间的距离为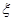 ,求随机变量
,求随机变量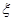 的分布列与数学期望
的分布列与数学期望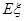 .
.